ответ: 13.5 кв.ед.
Объяснение:
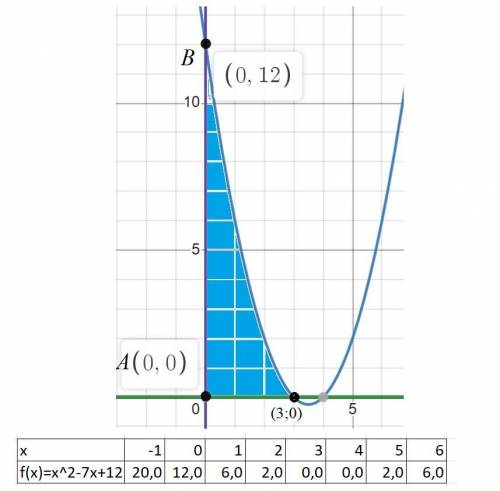
Строим графики функций
y=x^2-7x+12; y=0; x=0. (См. скриншот).
Площадь находим по формуле Ньютона-Лейбница
S(ABC) = ∫ₐᵇf(x)dx = F(x)|ₐᵇ = F(b) - F(a).
Пределы интегрирования находим по графику a=0; b=3.
f(x) = x^2-7x+12.
S(ABC) = ∫₀³(x^2-7x+12)dx = ∫₀³ x^2dx - 7∫₀³xdx + 12∫₀³dx = 13.5 кв.ед.
1) ∫₀³ x²dx = x³/3|₀³ = 1/3(3³-0³) = 27/3=9 кв.ед.
2) 7 ∫₀³xdx = 7(x²/2|₀³) = 7/2(3²-0²) = 63/2 = 31.5 кв.ед.
3) 12∫₀³dx = 12 (x|₀³) =12(3-0) = 12*3=36 кв.ед.
S(ABC) = 9-31.5+36 = 13.5 кв.ед.
Для нахождения точек экстремума функции f(x) = x^2√(1-x^2) нужно найти ее производную и приравнять ее к нулю:
f(x) = x^2√(1-x^2)
f'(x) = 2x√(1-x^2) - x^3 / √(1-x^2)
Теперь приравняем производную к нулю и решим полученное уравнение:
2x√(1-x^2) - x^3 / √(1-x^2) = 0
2x(1-x^2) - x^3 = 0
x(2-3x^2) = 0
Таким образом, точки экстремума функции находятся в точках x = 0, x = √(2/3) и x = -√(2/3).
Чтобы убедиться, что эти точки являются точками минимума или максимума, необходимо проанализировать знак производной в окрестности каждой точки. Можно использовать таблицу знаков, которая будет такой:
| x | -√(2/3) | 0 | √(2/3) |
|||||
| f'(x) | + | 0 | - |
| f(x) | - | 0 | + |
Таким образом, точка x = 0 является точкой минимума, а точки x = √(2/3) и x = -√(2/3) являются точками максимума.
9a^3 - a(3a+2)^2 + 4a(3a+7) = 9a^3 - a(9a^2+12a+4) + 12a^2 + 28a =
= 9a^3 - 9a^3 - 12a^2 - 4a + 12a^2 + 28a = 24a
При a = -1 1/16 = -17/16 будет 24a = -24*17/16 = -3*17/2 = -51/2 = -25,5