Рассмотрим произвольный прямоугольный треугольник АВС и проведем высоту СН = h из вершины С его прямого угла. Она разобьет данный треугольник на два прямоугольных треугольника АСН и ВСН; каждый из этих треугольников имеет с треугольником АВС общий острый угол и потому подобен треугольнику АВС. Все три треугольника АВС, АСН и ВСН подобны между собой. Из подобия треугольников АВС и АСН имеем СН2 = АН×ВН, т.е.
Теорема. Высота прямоугольного треугольника, опущенная из вершины прямого угла на гипотенузу, равна среднему геометрическому отрезков, на которые она разбивает гипотенузу.
h^2=m*n
a^2=c*m
b^2=c*n
c- гипотенуза
m и n - ее части
км/ч. 
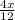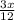км/ч, что на 20 км больше. - = 20
- 
= 20
=20
tg^2+1=tg^2+1
cos^2+1=-sin^2
sin^2+sin^2=2sin^2
sin^2-1=-cos^2
-cos^2=-cos^2