и 
то для площади и периметра получатся выражения:
;
;
;
;
;
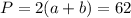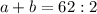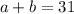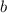в формулу для площади:
;
;
;
;
;
;
;
;
;
;
;
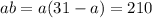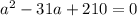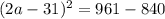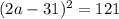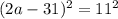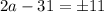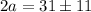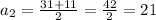м ;
м ; в формулу для :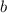
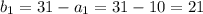м ;
м ;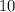
метров и 
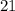метр.
Объяснение:
Если меньшая сторона прямоугольника - х см, то из условия большая сторона на 4 см больше, то есть (х+4), а диагональ - на 8 см больше, то есть (х+8).
Составляем уравнение исходя из теоремы Пифагора для прям. тр-ка, в котором гипотенуза - диагональ пр-ка, а катеты - его стороны:
(х+8)²= х² + (х+4)²
х² + 16х + 64 = х² + х² + 8х + 16
х² - 8х - 48 = 0
По теореме Виета корни:
х₁ = -4
х₂ = 12
Первый корень не подходит по смыслу. Значит меньшая сторона пр-ка равна 12.
Большая тогда равна 12+4 = 16 см.
ответ: 12см; 16 см.
56x⁴ - 45x² + 756 = 0
Сделаем замену x² = m ≥ 0
56m² - 45m + 756 = 0
D = (- 45)² - 4 * 56 * 756 = 2025 - 169344 = - 167319 < 0
Дискриминант меньше нуля ⇒ решений нет