Решением данной системы является пара чисел: 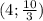 .
.
Объяснение:
Перед нами система уравнений с двумя неизвестными:
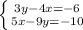
Данную систему уравнений проще решить, используя метод исключения одной переменной. Для этого домножим обе части первого уравнения на 3:
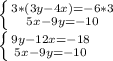
Теперь, сложим оба уравнения данной системы, чтобы избавиться от переменной y. Найдем x, путем упрощения обычного уравнения:
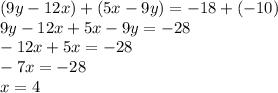
Теперь подставим данное значение в первое уравнение системы, чтобы найти y:
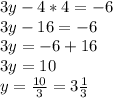
Получили ответ, что решением данной системы является пара чисел: 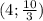
Пусть A1 — центр вписанной окружности ∆ SBC, B1 — центр вписанной окружности ∆ SAC, AA1 пересекается с A, A1, B1, B лежат в одной плоскости, значит прямые AB1 и BA1 пересекаются на ребре SC. Пусть точка пересечения этих прямых — p. Так как Ap и Bp — биссектрисы углов A и B, то . Но тогда AC • BS = BC • AS, отсюда , следовательно биссектрисы углов S в ∆ ASB и C в ∆ ACB пересекаются на ребре AB, т.е. точки S, C и центры вписанных окружностей ∆ ASB и ∆ ACB лежат в одной плоскости. Отсюда следует, что отрезки, соединяющие вершины S и C с центрами вписанных окружностей противолежащих граней, пересекаются.
t1=20 минут=1200 сек
t2=35 минут=2100 сек
Находим скорость: S1=V1*t
V=S1/t1=7000/1200=5*(5/6)
S2=V*t2=5*(5/6)*2100=8750 м=8,75 км