

1. С графика квадратичной функции.
x² + 3x - 18 < 0.
Рассмотрим функцию у = х² + 3х - 18. Графиком этой функции является парабола, ветви которой направлены вверх.
Выясним, как расположена эта парабола относительно оси Ох. Для этого решим уравнение х² + 3х - 18 =0:
D = 3² - 4 · 1 · (-18) = 9 + 72 = 81; √81 = 9
х₁ = (-3 + 9)/(2 · 1) = 6/2 = 3,
х₂ = (-3 - 9)/(2 · 1) = -12/2 = -6.
Значит, парабола пересекает ось Ох в двух точках, абсциссы которых равны -6 и 3.
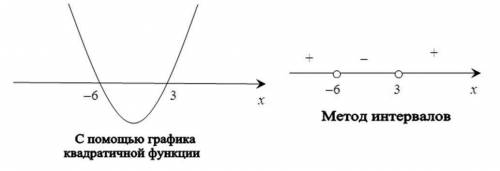
Покажем схематически, как расположена парабола в координатной плоскости (см. рис.) Из рисунка видно, что функция принимает отрицательные значения, когда х∈(-6; 3). Следовательно, множеством решений неравенства x² + 3x - 18 < 0 является промежуток (-6; 3).
2. Методом интервалов.
Метод интервалов применяется в случае, когда левая часть нервенства имеет многочлена, а правая равна 0. В этом случае находят корни многочлена, располагают их в порядке возрастания, наносят их на числовую ось, а затем справа налево располагают знаки "+" и "-", чередуя их, если корень некратный, и сохраняя знак, если корень кратный.
x² + 3x - 18 < 0
Разложим на множители многочлен x² + 3x - 18, для чего решим квадратное уравнение x² + 3x - 18 = 0:
D = 3² - 4 · 1 · (-18) = 9 + 72 = 81; √81 = 9
х₁ = (-3 + 9)/(2 · 1) = 6/2 = 3,
х₂ = (-3 - 9)/(2 · 1) = -12/2 = -6.
Значит, x² + 3x - 18 = (х - 3)(х + 6).
Отметим на координатной прямой точки -6 и 3 и укажем знаки многочлена на каждом из полученных интервалов (см. рис.).
Множество решений неравенства: х∈(-6; 3).
ответ:(-6; 3).
Дано неравенство: 6x² − x - 5 > 0.
Находим корни квадратного трёхчлена: 6x² − x - 5 = 0.
Квадратное уравнение, решаем относительно x:
Ищем дискриминант:
D=(-1)^2-4*6*(-5)=1-4*6*(-5)=1-24*(-5)=1-(-24*5)=1-(-120)=1+120=121;
Дискриминант больше 0, уравнение имеет 2 корня:
x1=(√121-(-1))/(2*6)=(11-(-1))/(2*6)=(11+1)/(2*6)=12/(2*6)=12/12=1;
x2=(-√121-(-1))/(2*6)=(-11-(-1))/(2*6)=(-11+1)/(2*6)=-10/(2*6)=-10/12=-(5/6)≈-0.833333.
откуда x1 = 1 и x2 = -(5/6).
Раскладываем левую часть неравенства на множители: 6(x – 1) (x +(5/6)) > 0. Точки -5/6 и 1 разбивают ось X на три промежутка:
ОО⟶Х
-5/6 1
Точки -5/6 и 1 выколоты. Это связано с тем, что решаемое неравенство — строгое (так что x не может равняться -5/6 или 1). Далее определяем знаки левой части неравенства на каждом из промежутков
+ – +
ОО⟶Х
-5/6 1
Получаем: x < -5/6 или x > 1.