ответ 80 км/ч на шоссе, и 100 км/ч на автостраде.
Объяснение:
Пусть х км/x - скорость на шоссе, тогда скорость на автостраде равна (x+20) км/ч
имеем уравнение:
+ 
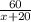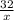=1 умножаем и левую и правую часть уравнения на x*(x+20)
60x + 32*(x+20)= x*(x+20)
60x + 32x + 640 = x^2 + 20x
x^2 + 20x - 60x - 32x - 640 = 0
x^2 - 72x - 640 = 0
D= 72^2 + 4*640 = 5184 + 2560 = 7744 = 88^2
x1=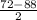
x1<0, а значит x1 не подходит по условию задачи.
x2=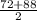
= 80 км/ч - скорость автомобиля на шоссе
тогда скорость на автостраде x+20= 80+20=100 км/ч
ответ 80 км/ч на шоссе, и 100 км/ч на автостраде.
0.16m^2 =4/25m^2=(2/5)^2m^2=(0.4m)^2
Для начала преобразуем десятичную дробь в обыкновенную:
0.16⇒16/100
Далее сокращаем дробь на 4 (Потому что и то и то делится на 4)
Делим 16 на 4 и 100 на 4. Получаем:
16/100=4/25 ⇒ Записываем 4/25 добавляя m^2 ⇒ 4/25m^2
Далее записываем число в виде степени с основанием 2/5 то-есть мы записываем 4/25 в таком виде (2/5)^2. Добавляем m^2 ⇒ (2/5)^2*m^2.
Последний шаг ⇒ перемножить члены с равными показателями путём умножения ⇒ (2/5)^2*m^2=(2/5m)^2
При делении 2 на 5 получим ⇒ 0.4. Соответственно записываем в ответ: (0.4m)^2
Или же можно решить по формуле: a^n*b^n=(ab)^n
0.16m^2 =0.4^2*m^2=(0.4m)^2
Представим 0.16 в виде 2 степени ⇒ 0.4^2
Применим формулу a^n*b^n=(ab)^n
0.4^2 это a^n а m^2 это b^n
Подставляем: 0.4^2*m^2
Умножаем: 0.4^2*m^2 и получаем (0.4m)^2
Пусть О(х; у;z) , А(х₁; у₁;z₁) , B(x₂;у₂;z₂)
Есть формула: х = (x₁ +x₂)/2; у = (у₁ + у₂)/2; z = (z₁ +z₂)/2
применим:
а) 5 = (3 + х₂)/2, ⇒ 10 = 3 + х₂, ⇒ х₂ = 7
б) 4 = (8 + у₂)/2, ⇒ 8 = 8 + у₂, ⇒ у₂ = 0
в) -2 = (2 + z₂)/2, ⇒ - 4 = 2 + z₂, ⇒ z₂ = -6
ответ: В(7;0;-6)
a. В(7; 0; -6)
b. В(4; 6; 0)
c. В(-7; 0; 6)
d. В(13; 16; -2)