![\sqrt[4]{47-2x}+\sqrt[4]{35+2x}=4](/tpl/images/0872/7193/19832.png)
ОДЗ:
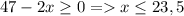
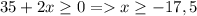
Общее ОДЗ: -17,5≤ x ≤23,5
Сумма 4 получается, если одно из слагаемых равно 3, а другое равно 1; или оба равны 2.
Рассмотрим все случаи
1 случай, когда первое слагаемое равно 1, а второе равно 3.
![\sqrt[4]{47-2x}=1;](/tpl/images/0872/7193/15be8.png) и
и ![\sqrt[4]{35+2x}=3;](/tpl/images/0872/7193/5f0d4.png)
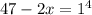
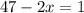
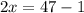
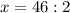
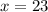
![\sqrt[4]{35+2x}=3;](/tpl/images/0872/7193/5f0d4.png)
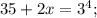
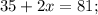
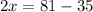
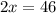
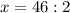
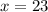
23=23
Получаем х₁=23
2 случай, когда первое слагаемое равно 3, а второе равно 1.
![\sqrt[4]{47-2x}=3;](/tpl/images/0872/7193/b7df8.png) и
и ![\sqrt[4]{35+2x}=1;](/tpl/images/0872/7193/d7b0a.png)
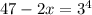
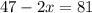
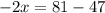
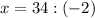
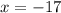
![\sqrt[4]{35+2x}=1](/tpl/images/0872/7193/4c301.png)
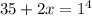
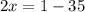
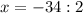
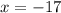
- 17= -17
Получаем х₂= -17
3 случай, когда первое и второе равны по 2.
![\sqrt[4]{47-2x}=2;\sqrt[4]{35+2x}=2](/tpl/images/0872/7193/723a3.png)
![\sqrt[4]{47-2x}=2;=47-2x=2^4](/tpl/images/0872/7193/b7fe7.png)
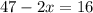
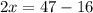
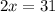
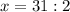
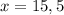
![\sqrt[4]{35+2x}=2=35+2x=2^4](/tpl/images/0872/7193/a2d5f.png)
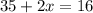
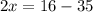

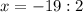
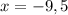
15,5 ≠ -9,5
ответ: х₁ = 23; х₂ = - 17
1)(5^(n-1))^2=5^(2n-2)-Так как при возведении степени в степень показатели степеней умножаются, а основание остается таким же.Пример:(a^(b))^c=a^(b*c).2n-2 Получаем умножая (n-1) на 2
2)5^(3n+7)=5^3n*5^7, Так как возьмем пример а^(b+c)=a^b*a^c
3)Перемножаем значения двух примеров
5^(2n-2)*5^(3n)*5^7.
Выделяем часть 5^(2n-2) и расскрываем скобки.Пример
a^(b-c)=a^b/a^c.В результате подставляя формулу получаем
5^(2n):5^2*5^(3n)*5^7=5^(2n-2+3n+7)=5^(5n+5)=5^5*5^n
Здесь мы решили действия со степенями при умножении степеней с одинаковым основанием, показатели степеней складываются, при делении, основание остается таким же, а показатели отнимаются.Приводим выражение.
4)Работаем со знаменателем
5^(5n+3)=5^(5n)*5^3 Принцип не объясняю, так как мы ранее с ним встретились
5)Делим числитель на знаменатель 5^5*5^n
----
5^(5n)*5^3
Сокращаем степени
5^(5+5n-(5n+3))=5^(5+5n-5n-3)=5^2=25
Скачай фотометч. Это будет решением всех твоих проблем)