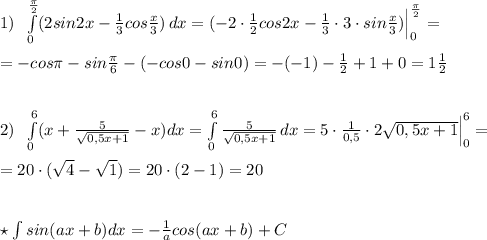
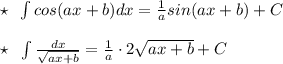
1)cos a = -0.5 в двух точках на единичной окружности , при а=2pi/3 и -2p/3
Учтем что период косинуса 2 пи, поэтому
pi(10x-7)/9=2pi/3+2pik ; (10x-7)/9=2/3+2k; 10x/9=2/3+7/9+2k;
x=9(13/9+2k)/10; x=1.3+1.8k; k-целое
наибольший отрицательный корень при к=-1
x1=1.3-1.8=-0.5
pi(10x-7)/9=-2pi/3+2pik; (10x-7)/9=-2/3+2k; 10x/9=-2/3+7/9+2k;
x=9(1/9+2k)/10; x=0.1+1.8k; k-целое
наибольшее из отрицательных при к=-1
x2=0.1-1.8=-1.7-меньше х1-не подходит
ответ x=-0.5
2)sin a=-√2/2 при a=-pi/4 и -3pi/4
такой же период 2пи
pi(2x-5)/2=-pi/4+2pik;(2x-5)/2=-1/4+2k; x=-1/4+5/2+2k; x1=9/4+2k=2.25+2k
наибольшее отрицательное при к=-2
x1=2.25-4=-1.75
pi(2x-5)/2=-3pi/4+2pik;(2x-5)/2=-3/4+2k; x=-3/4+5/2+2k; x2=7/4+2k=1.75+2k
наибольшее отрицательное при к=-1
x2=1.75-1=-0.25-больше х1, подходит
ответ x=-9.25
Объяснение:Найти производную следующих функций:
1) у = 4х^4 + 3х; y'= (4x⁴+3x)'= 16x³+3
2) у = 12х^2 - х – 2; y'= (12x²-x-2)' =24x - 1
3) у = -4х^9 - 8х^4 – 6х + 22; y' = (-4x⁹-8x⁴-6x+22)= - 36x⁸-32x³-6
4) у= 8х^7 - 14х^5 + 5х - 10; y' =(8x⁷-14x⁵+5x-10)'= 56x⁶-70x⁴+5
5) у = 6х^3 + (1/9)х^3 + 9х; y'= 18x²+(1/3)x²+9
6) у = 19х^4 + 3х^8 – 22. y'=76x³+24x⁷
«Производная степенной, логарифмической и показательной функций»
Найти производную следующих функций:
1. у = (х - 2)^8 y' = 8(x-2)⁷(x-2)'=8(x-2)⁷
2. у = (х2 + 2х)^3 y'= 3(x²+2x)²(x²+2x)'= 3(x²+2x)(x+2)=3x(x+2)²= 3x(x²+4x+4)=3x³+12x²+12x
3. у = (х +3)^4 y'=4(x+3)³(x+3)'= 4(x+3)³ =4( x³+9x²+27x+27)
4. у = 41^х y' = 41ˣ ln41
5. у = (3 + 5х + х3)^2 y' = 2( x³+5x+3)( x³+5x+3)'= 2( x³+5x+3)(2x+5)