Каждый час в первый бассейн наливается x м3 воды, во второй - x+22 м3. Очевидно, что эти 22 литра идут на погашение разницы в объёмах. То есть каждый час в первом бассейне 200 + n*x м3, во втором - 112 + n*x + 22*n, где n - количество часов. Через некоторое время объём воду в обоих бассейнах будет одинаков, т.е.
200 + n*x = 112 + n*x + 22*n
22*n = 88
n = 4
Через 4 часа объём воды в бассейнах будет одинаков.
1. -15 ≤ 1-2у ≤ 0
2. 
Объяснение:
1. Т.к. в линейном выражении 1-2у перед у стоит знак "-", то при вычислении пределов возможных значений нужно либо поменять направление знаков больше (меньше) либо поменять местами подставляемые значения 1/2 и 8.
для 1/2 ≤ у: 1-2у ≤ 0
для у ≤ 8: 1-2у ≥ -15
Тогда: -15 ≤ 1-2у ≤ 0
2. Здесь перед у знак "+", но появилась нелинейная зависимость 4/у, поэтому нужно вычислить производную функции (4/у + у) и приравнять её к нулю, чтобы найти ее экстремум.
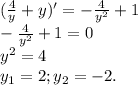
Но так как значение -2 не попадает в наш промежуток по условию, то это значение отбрасываем.
Значит, в точке у=2 имеем экстремум. Определим его значение:
для у=2: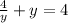 
.
На остальных участках функция либо возрастает, либо убывает. подставим граничные значения из условия:
для у=1/2 :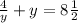 
для у=8: .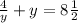
Т.е. имеем кривую с максимумами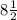 
и минимумом 4.
Тогда
Первоначальная разность объемов равна 200-112=88
время за которое покроется эта разность равна
88/22=4
ответ 4 часа