Дано: прямоугольный Δ
a; b - катеты
S=90 см²
S₁+S₂ = а²+b² =369 см₂
a-? b-?
Решение
1) Первое уравнение получаем из условия:
а²+b² = 369
2) Площадь прямоугольного треугольника равна половине произведения катетов, получаем второе уравнение:
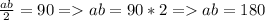
3) Решаем систему: (a>0; b>0)
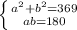
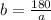
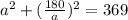
a≠0
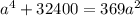
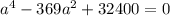
Замена: а²=t ( t > 0)
Решаем уравнение:
t² - 369t + 32400 = 0
D = 369² - 4·1·32400 = 136161 - 129600 = 6561 = 81²
t₁ = (369-81)/2 = 144
t₂ = (369+81)/2 = 225
Обратная замена:
При t₁ = 144 => a² = 144 => a₁ = - √144 = - 12 < 0
a₂ = √144 = 12 > 0
При t₂ = 225 => a² = 225 => a₃ = - √225 = - 15 < 0
a₄ = √225 = 15 > 0
Зная а₁=12 и а₂ = 15, найдем b
b₁ = 180/12 = 15
b₂ = 180/15 = 12
Получаем два решения взаимозаменяемых:
а=12; b=15
а=15; b=12
ответ: 12 см; 15 см - катеты
План-конспект урока
Алгебра
8 класс
Тема: Доказательство неравенств
Цель:
Образовательная: формирование умений доказательства неравенств, формирование
Этапы занятия:
Организационный момент.
Актуализация опорных занятий.
Усвоение новых знаний и действий.
Первичное закрепление знаний и действий.
Контроль и самопроверка знаний, рефлексия.
Подведение итогов занятий.
ХОД ЗАНЯТИЯ
1. Организационный момент. Подготовка учащихся к работе на занятии.
2. Подготовка к основному этапу. Обеспечение мотивации, значимости изучаемой темы занятия и принятия учащимися учебно-познавательной деятельности, актуализация опорных знаний.
а) С неравенств сравниваются большие и малые величины;
b) Во С какого приема мы умеем доказывать неравенство вида aответ:
- Один из приемов доказательства неравенства ab) сводят к доказательству равносильного ему неравенства a-b<0 (a-b>0);
c) Повторим данное доказательство на примере неравенства Коши.
“Среднее арифметическое неотрицательных чисел не меньше их среднего геометрического”:

Доказать: 
Доказательство: Рассмотрим разность левой и правой частей неравенства:

Неотрицательность квадрата любого вещественного числа очевидна.
Значит,  – верное неравенство.
3.
a) Во Попробуем сформулировать другой прием.
ответ (учитель ответить на во Другой прием состоит в том, чтобы показать, что данное неравенство является следствием некоторого очевидного неравенства:
(a-b)2  0, (a+b)2  0 или неравенства Коши  , при а0, b0, выражающее соотношение между средним арифметическим и средним геометрическим двух неотрицательных чисел;
b) Докажем, что (a+b)(ab+1)  4ab, при а0, b0.
Доказательство: Рассмотрим a+b и ab+1.
Используем очевидное неравенство Коши:

второго множителя.

Перемножим получившиеся неравенства:

с) Так же используют следующий прием: предполагают, что данное неравенство верно при заданных значениях переменных, строят цепочку неравенств-следствий, приводящую к некоторому очевидному неравенству. Рассматривая затем эту цепочку неравенств снизу вверх, показывают, что данное неравенство является следствием полученного очевидного неравенства и потому верно при указанных значениях переменных.
Значит, доказательство (a+b)·(ab+1)  4ab, при а0, b0 можно выполнить другим Допустим, что при а0, b0 данное неравенство верно, т.е.:

Используя неравенство Коши дважды для каждого множителя, имеем:

Значит, (a+b)·(ab+1)  4ab, при а0, b0, что и требовалось доказать.
4. Докажем: 
Доказательство: Допустим, что данное неравенство верно.

Получили очевидное неравенство.
Значит, данное неравенство  верно.
Во Мы можем привести доказательство данного неравенства из очевидного неравенства (a+b-2)2  0?
ответ: Да, для этого сделаем обратные шаги (рассказать по готовой записи)
Объяснение:
как то так, неуверен
2,5*3/6=2,5/2=1,25 (кг) муки.