A)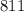 
Б)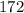 
Объяснение:
A)Трехзначные числа со средней цифрой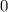 
имеют вид:
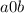
Цифра 
меняется от 
до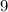 
, а цифра 
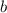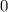от до .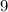
Таким образом, общее число чисел со средней цифрой 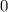равно: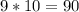 
Общее число трехзначных чисел :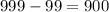 
Тогда, число трехзначных чисел со средней цифрой отличной от нуля:
.
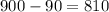Таким образом, чтобы среди взятых трехзначных чисел, наверняка было число со средней цифрой 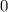, нужно взять: 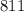трехзначных чисел.
Б) Определим общее число трехзначных чисел без нулей в десятичной записи.
На каждом из разрядов могут стоять цифры от до 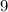(все кроме )
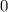Тогда, общее число таких трехзначных чисел: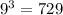 
Откуда, число трехзначных чисел содержащих ноль: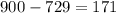 
Как видим, нужно взять как минимум : 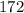трехзначных числа, чтобы среди них обязательно было число без нулей в десятичной записи.
Угол φ между двумя прямыми, заданными уравнениями c угловыми коэффициентами
y=k₁x+b₁ y=k₂x+b₂, вычисляется по формуле: tgφ=(k₂-k₁)/(1+k₁*k₂)
а) y=-3х/4-1 и y=3х/4 +2
tgφ=(3/4+3/4)/(1-9/16)=3*16/(2*7)=24/7=3 3/7
б) 2y+3x-1=0 и 3y+2x-5=0; у=-3х/2 -1/2и у=2х/3 +5/3;
tgφ=(2/3+3/2)/(1-(3*2)*(2/3)); tgφ=∞; φ=90°
в) x = 1 и y = -2x + 1;
cosφ=(1*2+0*1)/(√1*√5)=2/√5; sinφ=√(1-4/5)=1/√5; tgφ=(1/√5):(2/√5)=1/2
г) x = -3 и 3x + 2y - 3 = 0
cosφ=(1*3+0*2)/(√1*√(3²+2²))=3/√13; sinφ=√(1-9/13)=2/√13;
tgφ=(2/√13):(3/√13)=2/3