Окружность с центром в т. O и D = 68. Хорда AB.
Расстояние OM = 30 от т. O до прямой AB.
Найти:AB - ?
Решение:Заметим, что OM ⊥ AB (так как OM - это расстояние от т. О до прямой AB - длина перпендикуляра из точки О к прямой AB).
Пусть отрезок OM лежит на радиусе OC рассматриваемой окружности. Тогда OC, как радиус, перпендикулярный хорде, пересекает эту хорду ровно в ее середине: AM = BM.
Рассмотрим прямоугольные треугольники, равные по первому признаку (или же по двум катетам OM = OM и AM = BM): ΔAOM = ΔBOM.
OA = OB = D / 2 = 68 / 2 = 34, как радиусы.
OM = 30, по условию.
Применим теорему Пифагора, например, к ΔAOM:
AM² + OM² = AO²
AM² = AO² - OM²
AM² = 34² - 30²
AM² = 256
AM = 16
Значит:
AB = AM + BM = AM + AM = 16 + 16 = 32.
Задача решена!
ответ: 32.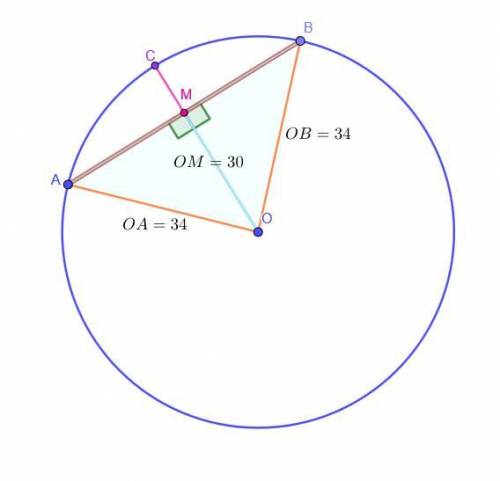
46 бусин. ЭТО ПРИМЕР ВСЁ СПИСЫВАТЬ НЕ НАД
Объяснение:
Всего: 57
Красных: 18
Зелёных: 18
Голубых: 15
Чёрных + белых: 57 - 18 - 18 - 15 = 6
Самая неудобная ситуация складывается, если мы достаём 13 красных, 13 зелёных, 13 голубых и 6 чёрных с белыми бусин. Это максимальное количество бусин, которое можно достать, при этом не получив 14 бусин одного цвета. Стоит достать ещё одну бусину, и мы можем быть уверены, что будет минимум 1 цвет минимум 14 бусин, а именно, нужно достать:
13 + 13 + 13 + 6 + 1 = 46 бусин.
ответ: 46 бусин.
2x+2y+x+y=72
3x+3y=72
3x=72-3y
разделить обе стороны уравнения на 3
x=24-y
ответ: x=24-у