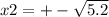
Парабола - это график квадратичной функции.
Она задается формулой у = ах² + bх + с (а ≠ 0).
Для построения графика квадратичноой функции существует алгоритм:
1. Найти координаты вершины параболы по формулам:
х₀ = -b/(2a); для нахождения у₀ нужно в формулу, которой задана функция, подставить вместо переменной х найденное значение х₀ и подсчитать, т.е. построить точку (х₀; у₀).
2. Записать уравнение оси симметрии параболы: х = х₀.
3. Найти координаты точек пересечения с осями координат:
с осью Оу: х = 0, у = с, т.е. точка (0; с);
с осью Ох: у = 0, решить уравнение ах² + bх + с = 0 и записать
координаты точек (если дискриминат D >= 0): (х₁; 0) и (х₂; 0).
Если у квадратного уравнения нет корней, т.е. график функции не пересекает ось Ох, то можно взять какие-нибудь дополнительные точки.
4. Построить точку, симметричную относительно оси симметрии точке пересечения с осью Оу.
Итак, для построения параболы хватит 5 точек.
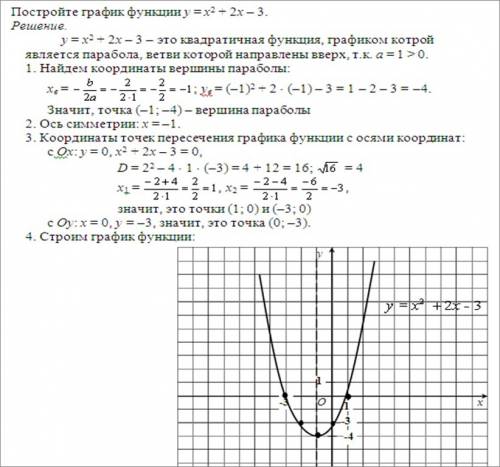
См. в качестве примера рисунок