ответ: 48.
Первый кол мы можем покрасить в любой из трех цветов (соблюдая условие задачи).
Второй кол мы можем покрасить только в 2 цвета (так как нам не следует соседние колья красить в один цвет).
Для третьего кола тоже остается 2 цвета (так как цвет 2-ого и 3-его кола не может совпадать).
С 4-ым и 5-ым колом похожая история: опять 2 цвета (для каждого из них).
А теперь, чтобы получить общее число нужно перемножить число для 1-ого, для 2-ого, ... , для 5-ого кольев:
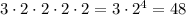
48 - это и есть ответ задачи!
1) -2(x - 3)² + 4. Чем больше будет значение х - 3, тем больше будет квадрат этого значения и тем более отрицательное число получится при умножении на минус 2. Так что х, при котором значение выражения максимальное, это 3.
-2(3 - 3)² + 4 = -2 · 0² + 4 = 0 + 4 = 4
2) -х² + 8х = 8х - х² = х(8 - х). Значение х не может превышать 8, так как иначе результат будет отрицательный, что точно нельзя будет назвать наибольшим значением выражения.
Подставим числа:
при х = 8: 64 - 64 = 0
при х = 7: 56 - 49 = 7
при х = 6: 48 - 36 = 12
при х = 5: 40 - 25 = 15
при х = 4: 32 - 16 = 16
при х = 3: 24 - 9 = 15
при х = 2: 16 - 4 = 12
при х = 1: 8 - 1 = 7
0 - 0 = 0
Как мы видим наибольшее значение данное выражение при х = 4. И это значение равно 16.
х=-3/(2 (а+1)).
Если знаменатель будет равна нулю, не будет решений, так как на 0 нельзя делить.
значит при а=-1 , нет решений.
при а не равно -1, имеется единственное решение.
Поэтому нет ни каких значений а, чтобы данное уравнения имело бесконечное множество корней.
ответ будет :нет таких а .