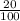 · a = 0,2a ⇒ c = 5a
· a = 0,2a ⇒ c = 5a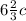 = 5c ·
= 5c · 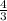 (5 ·
(5 · 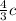 )
)1.(x,y)=(10,5) 2.(x,y)=( -1, -2) 3.(x,y)=( -5,0) 4.(x,y)=(5,1)
Объяснение:
1.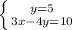 1.2(3+2y)+y=-4 1.-5+y-3y=-5 1.
1.2(3+2y)+y=-4 1.-5+y-3y=-5 1.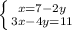
2.3x-4*5=10 2.y=-2 2.y=0 2.3(7-2y)-4y=11
3.x=10 3.x=3+2(-2) 3.x=-5+0 3.y=1
4.x=-1 4.x=-5 4.x=7-2*1
5.x=5
опытаемся найти точки их пересечения, решив систему:
(x-2) 2 + (y-3) 2=16
(x-2) 2 + (y-2) 2=4
(x-2) 2=16 - (y-3) 2
(x-2) 2=4 - (y-2) 2,
отсюда 16 - (y-3) 2=4 - (y-2) 2
16-у2+6 у-9=4-у2+4 у-4 ещё
6 у-4 у=4-4+9-16 ещё
2 у=-7 найдём игрек
у=-3,5 и попробуем найти икс
(x-2) 2=4 - (-3,5-2) 2
(x-2) 2=4-30,25
(x-2) 2=-25,75, а квадрат не может быть отрицательным, следовательно, эти две окружности не пересекаются. центры окружностей - в точках (2; 3) и (2; 2) соответственно, то есть расстояние между центрами равно единице, а радиусы - 4 и 2, то есть вторая, меньшая, окружность расположена внутри первой.
ответ: малая окружность расположена внутри большой.
Какой это может быть делитель: 2 не может быть, тогда число а будет равно 10, а число b может быть только 2 (чтобы общим наибольшим делителем было число 2), тогда наибольший общий делитель 2 будет составлять 100% от числа b, а такого ответа у нас нет. Перебирая таким образом все возможные общие делители при сохранении всех условий задачи, делаем выводы, что правильный ответ: 25 %. Как пример можно привести: а = 15, b = 12, наибольший общий делитель - 3.
ответ: 25 % (вариант Д).