
0<x<4/3
Объяснение:
числитель является положительным (это число 7, от x не завист)
надо найти значения x, при которых знаменатель положителен:
4 × x - 3 × x**2 > 0
4 × x - 3 × x**2 = x × (4 - 3×x)
рассмотрим 2 случая:
1. Оба положительные ( и x, и (4 - 3×x)): одновременно должно выполняться:
x > 0 и 4 - 3 × x > 0
x > 0 и -3×x > -4
x > 0 и x < 4/3
в этом случае решение существует. А именно,
0<x<4/3
2. Оба отрицательные: одновременно должно выполняться:
x < 0 и 4 - 3×x < 0
x < 0 и -3 × x < - 4
x< 0 и x> 4/3
в этом случае решения не существует.
Оставляем первый случай.
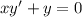
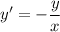 - уравнение с разделяющимися переменными
- уравнение с разделяющимися переменными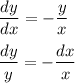
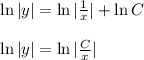
 - общее решение
- общее решение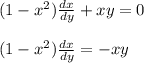

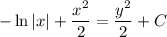 - общий интеграл
- общий интеграл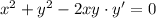

 , тогда
, тогда 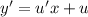



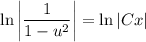
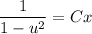
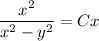 - общий интеграл
- общий интеграл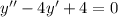
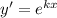 , тогда будем иметь характеристическое уравнение следующего вида:
, тогда будем иметь характеристическое уравнение следующего вида:
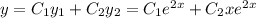 - общее решение
- общее решение
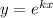 , тогда получаем
, тогда получаем
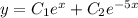

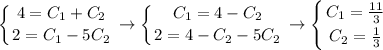
 - частное решение
- частное решение
б)
-x²-10x-25,
D=100-100=0,
x=
-x²-10x-25=-(x+5)(x+5) по формуле разложения квадратного трехчлена;
в)