Вероятность того, что взятая деталь будет деталью с 1 верстака равна:
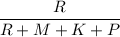, где 
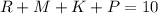- общее число деталей.
Вероятность того, что взятая деталь будет небракованной деталью с 1 верстака равна:
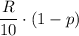, где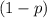 
- вероятность того, что деталь с 1 верстака небракованная (противоположное событие по отношению к бракованной детали)
Для остальных верстаков вероятности рассчитываются аналогичным образом:
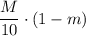- вероятность того, что взятая деталь будет небракованной деталью со 2 верстака равна
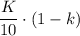- вероятность того, что взятая деталь будет небракованной деталью с 3 верстака равна
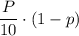- вероятность того, что взятая деталь будет небракованной деталью с 4 верстака равна
Тогда, вероятность того что наугад взятая деталь не будет бракованной будет рана сумме четырех вероятностей. так как рассмотренные события являются несовместными (деталь не может быть с нескольких верстаков одновременно):
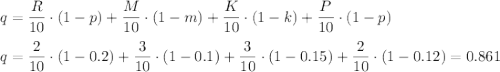
Вероятность того что наугад взятая деталь небракованная и взятая с 1 верстака уже рассматривалась:
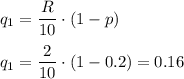
ответ: 0.861; 0.16
один и множителей равен 15 ⇒ произведение делится на 15