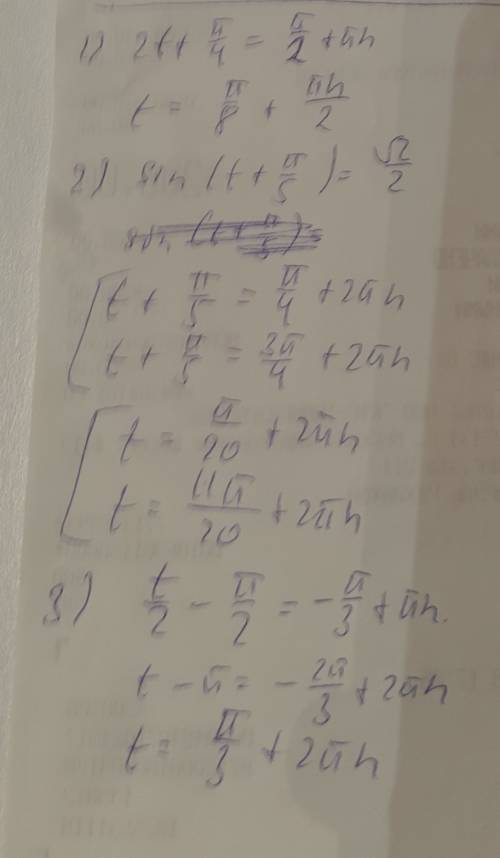
Решение
KLMN - ромб (все стороны равны).
Площадь ромба равна половине произведения диагоналей,
диагонали ромба - равны сторонам прямоугольника,
поэтому площадь ромба равна половине площади прямоугольника.
Ромб разделен на три треугольника MNP, NKP и MPL.
Площадь треугольника MNP равна сумме площадей NKP и MPL,
так как основание треугольника MNP - MN, равно сумме оснований NKP и MPL - KP и PL, а высоты, проведенные к этим основаниям равны . Значит, площадь треугольника MNP равна половине площади ромба KLMN и четверти площади прямоугольника ABCD.
Площадь треугольника MNP = 36/4 = 9.
ответ: 9

ОДЗ: 

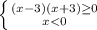
+ - +
////////////////////////-3_________________3/////////////////////////////////////
x∈ (-∞; -3]∪[3; +∞)
- +
\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\\0__________________________
x∈(-∞; 0)
Общее решение:  иначе x∈(-∞; -3]
иначе x∈(-∞; -3]
ответ: x∈(-∞; -3]
1) так как cos(t) = 0 для t = π/2 +kπ, k=z то
2t+π/4=π/2 + kπ, k=z
2) переносим константу в правую часть равенства
2t+π/2-π/4 + kπ, k=z
3) решаем уравнение
t=π/8+kπ/2, k=z
ВТОРОЕ УРАВНЕНИЕ:
t= π/20+2kπ
11π/20+2kπ
k=z
ТРЕТЬЕ УРАВНЕНИЕ:
t= π/3+2kπ, k=z