Декартовы координаты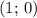 
на числовой окружности имеет угол 
.
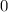Декартовы координаты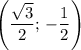 
на числовой окружности имеет угол 
.
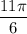Учитывая, что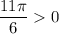 
и то, что поворот против часовой стрелки является движением в положительную сторону на числовой окружности, находим угол поворота:
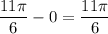
Но, так как длина одного полного оборота по числовой окружности равна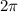 
, то, пройдя еще некоторое количество кругов в ту же сторону, мы попадем снова в исходную точку. Поэтому, все искомые углы определяются формулой:
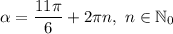, где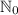 
- множество целых неотрицательных чисел
Переведем углы в градусную меру:
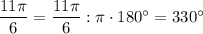
Получим новую запись:
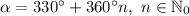
1)при пересечении графика с осью ОХ у=0 0=4х-2 4х=2 х=2:4 х=0,5
(0,5;0) т.пересечения с ОХ
при пересечении графика с осью ОУ х=0 у=4*0-2=-2
(0;-2) т.пересечения с ОУ
2) чтобы найти т.пересечения графиков надо приравнять правые части этих функций 2,8х-5=1,2х+7 и решить это уравнение
2,8х-1,2х=7+5
1,6х=12
х=12:1,6
х=7,5 подставим значение в любую функцию
у=2,8*7,5-5=21-5=16
(7,5;16) это координаты точки пересечения графиков функций y=2,8x-5 и y=1,2x+7
2*(-3)²+7*(-3)+с=0 спростимо
18-21+с=0 знайдемо цешку
с=3.
Отже, наше ривняння маэ вигляд:
2х²+7х+3=0 роздилимо його на два
х²+3,5х+1,5=0 и роздилимо вильний член на перший коринь
х2=1,5/-3=-0,5.
Видповидь: с=3; х2=-0,5.