2015 год - не високосный. значит в феврале 28 дней.
Всего в зимние месяцы, декабрь 31 , янваарь 31 и февраль 28 - 90 дней.
если принять 90 дней в году, как выборку, тогда у нас есть 2 варианты: 29 дней, когда шел снег и 90-29=61 день - без осадков.
Сумма вариант всегда равна числу выборки: 29+61=90
Сумма относительных частот всегода = 1 или 100%
Обозначим: n=90
m₁=29
m₂=61
Относительная частота(W) - это отношение варианты к выборке: W=m/n
29/90=0.3(2)≈32%
100%-32%=68%
Проверка: 61/90=0.6(7)≈68%
1-0.6(7)=0.3(2)
ответ: Относительная частота дней без осадков = 68%
Объяснение:
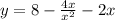
На 0 делить нельзя. Область определения: (-∞;0)∪(0;∞)
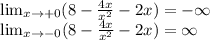
Т.к х не равен 0, то точек пересечения с осью у нет. Находим точки пересечения с осью х.
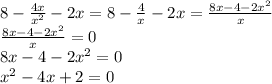
Решаем квадратное уравнение, находим точки пересечения с осью х:
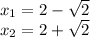
Находим точки экстремума (производная равна нулю).
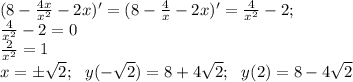
Для нахождения точек перегиба находим вторую производную
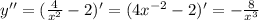
Вторая производная нигде не равна нулю, точек перегиба нет.
Горизонтальных асимптот нет. Вертикальная асимптота одна: х=0.
Ищем наклонную асимптоту:
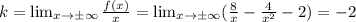
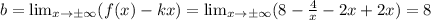
Наклонная асимптота есть:
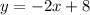
Дальнейшее исследование проводим, заполняя таблицу (см. рис.1).
a40=?
an=a1+d(n-1);
a40=-8+2(40-1)=-8+2*39=-8+78=70