Объяснение:
Чтобы не путать русскую букву "З" с цифрой "3" - запишем пример в виде:
R A Z
+
A Z
+ Z
______
4 4 4
1)
Получили, что
Z + Z + Z = 4; 3×Z = * 4
Здесь один вариант: Z = 8: 3×4 = 24
2)
Из разряда единиц переносим двойку в разряд десятков.
Получим:
2 + 2×A = *4
Простым подбором получаем;
A = 1; 2 + 2×1 = 04
A = 6; 2 + 2×6 = 10
То есть если нет переноса в разряд сотен, то
R + 0 = 4; R = 4
Если есть, то:
R + 1 = 4; R = 3.
Возвращаемся к прежним обозначениям.
Получили 2 ответа:

Биквадратное уравнение.
Решается заменой переменной:

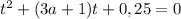
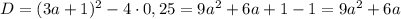
Если D >0, т.е.


уравнение имеет корни:
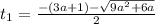 или
или 
Обратный переход:
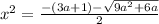 или
или 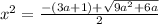
Уравнение x^2=с имеет корни, если c> 0, тогда корни противоположны по знаку
Чтобы корни данного уравнения были равны,
с=0
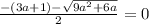
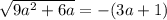
Это иррациональное уравнение.
При (3a+1) >0 оно не имеет корней.
При (3а+1) ≤0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Аналогично
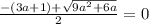
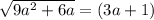
При (3a+1) < 0 оно не имеет корней.
При (3а+1) ≥0
возводим обе части уравнения в квадрат:

0=1 - неверно, нет таких значений а
Если  , т.е
, т.е 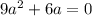
 или
или 
При 
уравнение принимает вид:

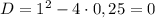 ⇒
⇒ 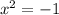
уравнение не имеет корней
При 
уравнение принимает вид:

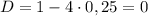 ⇒
⇒ 
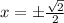
Уравнение 4-ой степени, значит
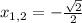 и
и 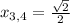
О т в е т. При 