Пояснение:
1) Если максимально просто объяснять, то когда одинаковые значения , а степени могут быть одинаковые или разные , умножаются , например как тут:
*
, то их степени суммируются , т.е. 
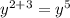
2) А при делении наоборот степени вычитаются, например :
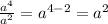, т.е. от значения степени числителя 
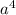вычитаем значение знаменателя 
.
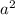3) Есть ещё 1 пример, это когда имеется степень за скобкой, типа 
, то тут степени умножаются друг на друга и у нас выйдет так:
Теперь решение:
Задача состоит в том, чтобы вместо точек подставить такое значение со степенью, чтобы получилось равенство.
1)
- такие действия буду пропускать, как раз потренируешься.
* 
= 
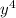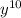- для того, чтобы получить 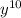, нужно вместо точек вставить , тогда даст 
, и 4+6=10 => 
=
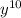
2)
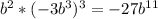
3)
4)
5)
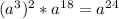
Если посмотришь на свойства степеней, то узнаешь ещё больше , чтобы быть всегда на готове.
(6a-7-(4a-2))×(6a-7+(4a-2))
(6a-7-4a+2)×(6a-7+4a-2)
(2a-5)×(10a-9)