1)
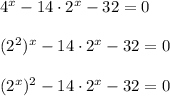
Введём замену: 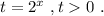
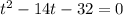
По теореме Виета:
 .
.
Но так как 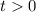 , то -2 не является решением этого уравнения. Выполняем обратную замену:
, то -2 не является решением этого уравнения. Выполняем обратную замену:
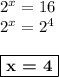
ответ: 4.
2)
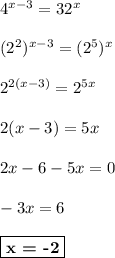
ответ: -2.
3)
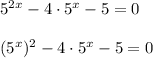
Введём замену: 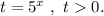
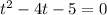
По теореме Виета:

Но так как 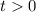 , то -1 не является решением этого уравнения. Выполняем обратную замену:
, то -1 не является решением этого уравнения. Выполняем обратную замену:
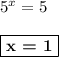
ответ: 1.
4)
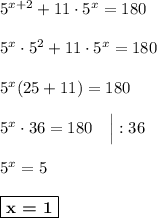
ответ: 1.
5)
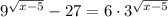
Для начала кое-что учтём: подкоренное выражение всегда неотрицательно. То есть:
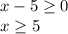
Продолжаем решение:

Введём замену: 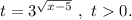
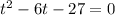
По теореме Виета:

Но так как 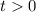 , то -3 не является решением этого уравнения. Выполняем обратную замену:
, то -3 не является решением этого уравнения. Выполняем обратную замену:
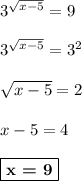
ответ: 9.
y = -0,25x^2 + 2x +5
С осью Ох:
y = 0
- 0,25x² + 2x + 5 = 0
x² - 8x - 20 = 0
x₁ = - 2
x₂ = 10
(- 2;0) ; (10;0)
С осью Оу:
x = 0
y = 5
(0;5)