Функция задана формулой у=5,6х найдите значение х если у=16,8

👇

Увидеть ответ

Ответ:

лизалол

10.04.2022

X = y/5.6
Подставляем:
x = 16.8/5.6 = 3

4,8(3 оценок)

Открыть все ответы

Ответ:

sofiaivkina84

10.04.2022

Метод Феррари:

уравнение вида

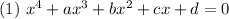
$(1)\ x^4+ax^3+bx^2+cx+d=0$

с замены 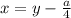$x=y-\frac{a}{4}$

приводим к виду

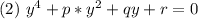
$(2)\ y^4+p*y^2+qy+r=0$

где:

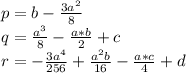
$p=b-\frac{3a^2}{8}\\q=\frac{a^3}{8}-\frac{a*b}{2}+c\\r=-\frac{3a^4}{256}+\frac{a^2b}{16}-\frac{a*c}{4}+d$

добавим и вычтем из левой части уравнения 2 выражение 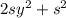2sy^2+s^2 , где s - некоторое число: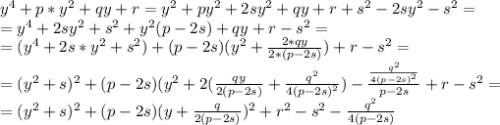 $y^4+p*y^2+qy+r=y^2+py^2+2sy^2+qy+r+s^2-2sy^2-s^2=\\=y^4+2sy^2+s^2+y^2(p-2s)+qy+r-s^2=\\=(y^4+2s*y^2+s^2)+(p-2s)(y^2+\frac{2*qy}{2*(p-2s)})+r-s^2=\\=(y^2+s)^2+(p-2s)(y^2+2(\frac{qy}{2(p-2s)}+\frac{q^2}{4(p-2s)^2})-\frac{\frac{q^2}{4(p-2s)^2}}{p-2s}+r-s^2=\\=(y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2+r^2-s^2-\frac{q^2}{4(p-2s)}$

получим:

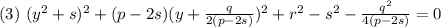
$(3)\ (y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2+r^2-s^2-\frac{q^2}{4(p-2s)}=0$

Пусть s - корень уравнения

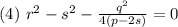
$(4)\ r^2-s^2-\frac{q^2}{4(p-2s)}=0$

Тогда уравнение 3 примет вид:

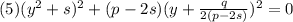
$(5)(y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2=0$

Избавляемся в уравнении 4 от знаменателя:

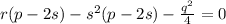
$r(p-2s)-s^2(p-2s)-\frac{q^2}{4}=0$

Раскроем скобки и получим:

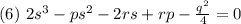
$(6)\ 2s^3-ps^2-2rs+rp-\frac{q^2}{4}=0$

Уравнение 6 называется кубической резольвентой уравнения 4 степени.

Разложим уравнение 5 на множители:

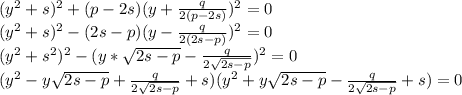
$(y^2+s)^2+(p-2s)(y+\frac{q}{2(p-2s)})^2=0\\(y^2+s)^2-(2s-p)(y-\frac{q}{2(2s-p)})^2=0\\(y^2+s^2)^2-(y*\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}})^2=0\\(y^2-y\sqrt{2s-p}+\frac{q}{2\sqrt{2s-p}}+s)(y^2+y\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}}+s)=0$

Получим два квадратных уравнения:

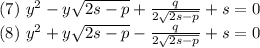
$(7)\ y^2-y\sqrt{2s-p}+\frac{q}{2\sqrt{2s-p}}+s=0\\(8)\ y^2+y\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}}+s=0$

Применяем этот метод для решения уравнения:

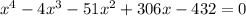
$x^{4} -4x^{3} -51x^{2} +306x-432=0$

коэффициенты:

a=-4

b=-51

c=306

d=-432

Определяем p,q и r:

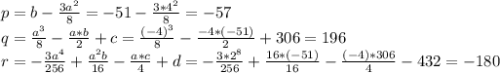
$p=b-\frac{3a^2}{8}=-51-\frac{3*4^2}{8}=-57 \\q=\frac{a^3}{8}-\frac{a*b}{2}+c=\frac{(-4)^3}{8}-\frac{-4*(-51)}{2}+306=196 \\r=-\frac{3a^4}{256}+\frac{a^2b}{16}-\frac{a*c}{4}+d=-\frac{3*2^8}{256} +\frac{16*(-51)}{16} -\frac{(-4)*306}{4} -432=-180$

Ищем s:

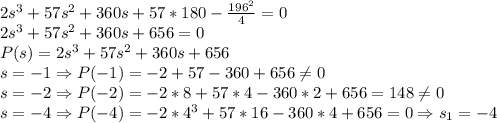
$2s^3+57s^2+360s+57*180-\frac{196^2}{4}=0\\2s^3+57s^2+360s+656=0\\P(s)=2s^3+57s^2+360s+656\\s=-1\Rightarrow P(-1)=-2+57-360+656\neq 0\\s=-2\Rightarrow P(-2)=-2*8+57*4-360*2+656=148\neq 0\\s=-4\Rightarrow P(-4)=-2*4^3+57*16-360*4+656=0 \Rightarrow s_1=-4$

Возможно, у этого уравнения третьей степени есть и другие действительные корни. Но для данной задачи находить их все не обязательно. Достаточно одного корня, т.е числа, при котором выражение обращается в ноль.

Подставляем p,q,r и s в квадратные уравнения 7 и 8:

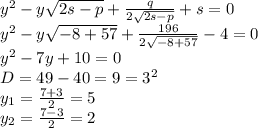
$y^2-y\sqrt{2s-p}+\frac{q}{2\sqrt{2s-p}}+s=0\\y^2-y\sqrt{-8+57}+\frac{196}{2\sqrt{-8+57}} -4=0\\y^2-7y+10=0\\D=49-40=9=3^2\\y_1=\frac{7+3}{2}=5\\y_2=\frac{7-3}{2}=2$

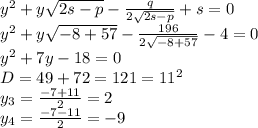
$y^2+y\sqrt{2s-p}-\frac{q}{2\sqrt{2s-p}}+s=0\\y^2+y\sqrt{-8+57}-\frac{196}{2\sqrt{-8+57}} -4=0\\y^2+7y-18=0\\D=49+72=121=11^2\\y_3=\frac{-7+11}{2}=2\\y_4=\frac{-7-11}{2}=-9$

Находим x:

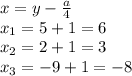
$x=y-\frac{a}{4} \\x_1=5+1=6\\x_2=2+1=3\\x_3=-9+1=-8$

ответ: -8; 3; 6

4,4(99 оценок)

Ответ:

Гашин

10.04.2022

Не знаю, где ты тут высшую математику нашел, программа 9 класса. Монотонность сам уже не помню что такое, а точки экстремума находишь через производную.

Давай второй номер тебе сделаю.

y= x^2-2x+9

y' = (x^2)' -(2x)' + (9)'//Взяли производную и дальше приравниваем ее к нулю и находим корни.

Но можно и проще.

У нас дан график параболы с ветвями вверх( икс положительный), значит точка экстремума будет минимальное значение икса на параболе. Вычисляется по формуле x= (-b)/2a

x= 2/2=1

Если я чего-то не напутал, то вроде так.

Объяснение:

4,7(95 оценок)

Это интересно:

Хобби-и-рукоделие

18.12.2020

Как быстро размягчить пластилин Playdough: 5 простых способов...

Кулинария-и-гостеприимство

03.04.2023

Узнай, как сделать невероятно вкусный и загадочный мартини драгон...

Здоровье