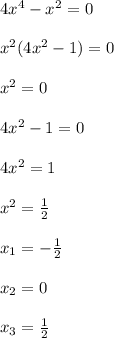
Задание 5:
Ну смотри, у тебя 5 открыток и 5 ветеранов, значит
первому ветерану ты можешь отправить 1 из 5 открыток
второму ветерану ты можешь отправить 1 из 4 открыток
...
пятому ветерану ты можешь отправить только одну открытку
и получается, что: 5*4*3*2*1=120 (вариантов)
мы их перемножаем, потому что вариаций с тем, кому попадет та или иная открытка много
Задание 6:
если цифры не повторяются, то мы действуем по тому же принципу, что и в задании 5:
на первое место могут пойти любые 3 цифры
на второе место только 2 из оставшихся
ну и на 3 - последнее
и получаем: 3*2*1=6
Задание 7:
все по тому же принципу))
первое место могла занять любая из 4 команд
второе место - любая из 3
...
ну и 4 место - та, что осталась
получаем: 4*3*2*1=24
Задание 8:
а вот тут я не знаю, прости)
11 в любой степени кончается на 1. 19 в нечетной степени кончается на 9.
Их сумма кончается на 1+9=10, то есть на 0, а значит, делится на 5.
Осталось доказать, что это число делится на 3.
11=3*3+2; 11^2019 = (3*3+2)^2019 = 2^2019.
Здесь и дальше знак = означает "такой же остаток при делении на 3".
2^2019 = (2^3)^673 = 8^673 = 2^673 = 2^3*2^670 = 8*(2^10)^67 = 2*1024^67 =
= 2*(3*341+1)^67 = 2*1^67 = 2
Таким образом, 11^2019 имеет при делении на 3 остаток 2.
19 = 3*6+1; 19^2019 = (3*6+1)^2019 = 1^2019 = 1.
Таким образом, 19^2019 имеет при делении на 3 остаток 1.
Сумма этих чисел имеет остаток 2+1=3, то есть делится нацело.
Что и требовалось доказать.
x^2 (4x^2 - 1) = 0
x^2 = 0
x = 0
4x^2 - 1 = 0
4x^2 = 1
x^2 = 1/4
x = ± √ (1/4)
x = ± 1/2
ОТВЕТ
- 1/2; 0; 1/2