Объяснение:
Для того, чтобы найти решение системы:
3x + 8y = 13;
5x - 16y = 7,
нам удобнее всего будет применить метод сложения. Рассмотрев оба уравнения мы видим, что перед переменной y в обеих уравнениях мы можем сделать взаимно противоположными коэффициенты.
Умножаем на 2 первое уравнение системы:
6x + 16y = 26;
5x - 16y = 7.
Сложим два уравнения системы:
6x + 5x = 26 + 7;
8y = 13 - 3x;
Решим первое уравнение:
6x + 5x = 33;
11x = 33;
x = 33 : 11;
x = 3.
Система уравнений:
x = 3;
y = (13 - 3 * 3)/8 = (13 - 9)/8 = 4/8 = 1/2.
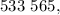 которая должна выражать дату (в каком-то неизвестном представлении).
которая должна выражать дату (в каком-то неизвестном представлении).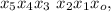


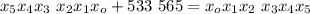 ;
;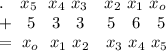

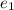 – возможная добавочная единица, уходящая из первого
– возможная добавочная единица, уходящая из первого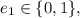
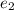 – возможная добавочная единица, уходящая из второго
– возможная добавочная единица, уходящая из второго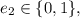
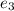 – возможная добавочная единица,
– возможная добавочная единица,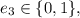
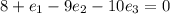 ;
;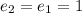 и при
и при  ;
;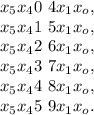
 поскольку
поскольку 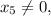 так как с этой цифры начинается разностное число.
так как с этой цифры начинается разностное число. поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.
поскольку в первом разряде уже есть шестёрка и добавочная единица, получаемая из нулевого разряда.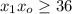 .
.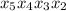 .
.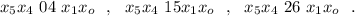
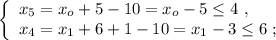

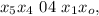
 может играть роль апреля.
может играть роль апреля.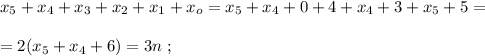
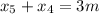 ;
;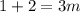 ;
;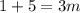 ;
;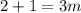 ;
; ;
;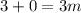 ;
;
 – дата 12/04/56 г.
– дата 12/04/56 г. – дата 15/04/86 г.
– дата 15/04/86 г.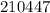 – дата 21/04/47 г.
– дата 21/04/47 г.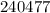 – дата 24/04/77 г.
– дата 24/04/77 г.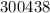 – дата 24/04/38 г.
– дата 24/04/38 г.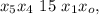
 может играть только роль числа месяца (дня).
может играть только роль числа месяца (дня).
 ;
;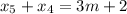 ;
;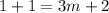 ;
;
 – дата 11/15/46 г.
– дата 11/15/46 г.

1) (х-3y)²= х²- 2·х·3у+(3у)²= х²-6ху+9у²
2) (х+4y)(4y-x)= (4y-x)(х+4y)= (4у)²-х²=16у²-х²
3) х²-6ху+9у² + 16у²-х² = 25у² - 6ху