2x² + 7x - 4 = 0
Это квадратное уравнение решения много, самый частый -- через дискриминант (D).
Квадратное уравнение в общем виде выглядит так:
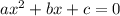
где a, b, c -- коэффициенты, a ≠ 0
Формула дискриминанта:
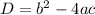
Формула корней:
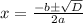
При этом от дискриминанта зависит количество корней в уравнении:
Если D > 0, то уравнение имеет 2 корня
Если D = 0, то уравнение имеет 1 корень
Если D < 0, то уравнение не имеет корней
Теперь решение:
2x² + 7x - 4 = 0
В нём a = 2, b = 7, c = -4. Подставим эти значения в формулу дискриминанта:
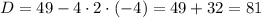
D > 0, значит уравнение имеет 2 корня.
Найдём корень из дискриминанта и корни уравнения:
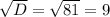
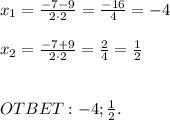
тогда точка пересечения с осью y будет точка (0;5).
Точки пересечения с осью х, их по другому еще называют нули функции.
Для того чтобы найти точки пересечения с осью х, точно все выражение приравнять к нулю.(или другими словами у=0)
Тогда :
x^2-6x+5=0
(Решаем через дискриминант)
Д=(b)^2-4ac
Д=36-20=16; Д>0,то будет 2 корня.
x1= (6+4)/2=10/2=5
x2=(6-4)/2=2/2=1
Тогда точки пересечения с осью х будут точки:
х1=1, x2=5
ответ:
с осью оу точка: (0;5)
с осью х точки: (1;0) и (5;0)