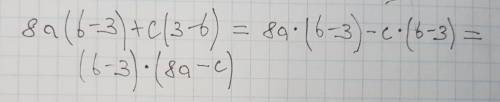
объяснение:
№5 если в выпуклом четырёхугольнике диагонали равны и равны две противоположные стороны, то по признаку он или прямоугольник, или квадрат, или равнобокая трапеция.
в прямоугольнике и в квадрате диагонали,пересекаясь, делятся пополам, ⇒ ао=до, как половины равных отрезков.
если имеем равнобокую трапецию,то из равенства треугольников, имеющих своими сторонами основание ад и диагонали, получим равные угла между диагоналями и основанием ад ⇒δаод- равнобедренный и ао=од (замечание: чертёж, представленный в неверен, т.к. диагонали преломляются).
№6. т.к. противоположные стороны попарно равны ⇒ четырёхугольник - параллелограмм по признаку ⇒ диагонали точкой пересечения делятся пополам по свойству диагоналей параллелограмма.
75°
Объяснение:
По условию считаем, что каждый друзей видит свой участок стены и друзья вместе контролируют только четвертую часть стены комнаты, что означает 90° (рисунок приложен). По обозначению эта стена дуга BE= дуга EC + дуга СВ = 90°.
Угол обзора одного из друзей ∠CDE=10°, а у другого ∠ВАС=20°, а их сумма ∠ВАС+∠CDE=10°+20°=30°.
Нужно определить градусную меру щели КМ, т.е. дуги КМ.
Применим следующую теорему о секущих:
Угол между двумя секущими, проведенными из одной точки, равен полу разности большей и меньшей высекаемых ими дуг.
Тогда ∠ВАС=(дуга СВ - дуга КМ)/2 и ∠CDE=(дуга EC - дуга КМ)/2.
Поэтому
∠ВАС+∠CDE=(дуга СВ - дуга КМ)/2+(дуга EC - дуга КМ)/2=
=(дуга EC + дуга СВ - 2•дуга КМ)/2=(90°-2•дуга КМ)/2
или же
(90°-2•дуга КМ)/2=30°
90°-2•дуга КМ = 60°
2•дуга КМ = 150°
дуга КМ = 150° : 2 = 75°.
