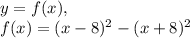
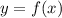— прямая пропорциональность.
— прямая пропорциональность, то есть доказать, что в выражении 
находится в первой степени 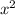(не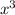 
, не 
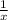, не 
и не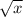 
, а просто ).. Если внимательно посмотреть это выражение можно видоизменить по формулам сокращенного умножения, а именно по формуле «разность квадратов». Действительно, данное выражение имеет вид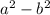 
, где 
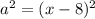, и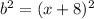 
. Формула «разность квадратов» раскрывается так: 
.
.
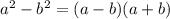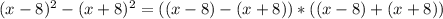
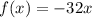, находится в первой степени, а значит зависимость — есть прямая пропорциональность. Доказано.
Объяснение:
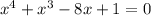
Выделим полную четвертую степень:
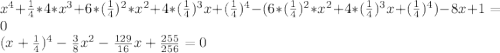
Сделаем замену: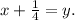 
Откуда: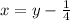 
Уравнение примет вид:
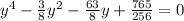
Домножим обе части уравнения на 256 и сделаем замену m = 4y;
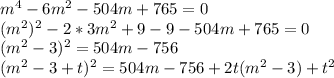, где t - такое число, которое сворачивает правую часть в полный квадрат. Его следует найти, рассмотрев квадратный трехчлен относительно m и найдя его дискриминант и приравняв его к нулю:
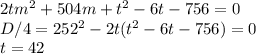- корень. Значит, можно разделить данный трехчлен на (t - 42), получим:
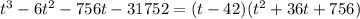
Очевидно, второй множитель не имеет действительных решений. Значит, t = 42. Напомню, что это такое число, при котором правая часть - полный квадрат. Подставим его.
^2 = (2\sqrt{21} (m+3))^2](/tpl/images/0545/9419/8a540.png)
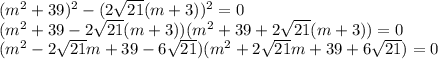
Рассмотрим первый множитель:
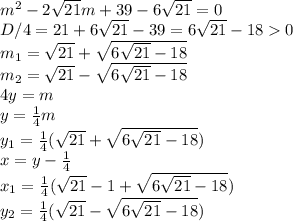
Аналогично рассмотрев второй множитель обнаружим, что D/4 < 0, а значит, действительных корней нет.
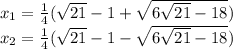
8z<-8-16
8z<-24
z<-3
Из всех чисел, лишь -8 меньше -3.
ответ: -8