Question

Решить производные

1) y =

2) y=

3) y=

Answer 1

$1)y=\sqrt[5]{x}+x\sqrt[3]{x}=x^{\frac{1}{5}}+x*x^{\frac{1}{3}}=x^{\frac{1}{5}}+x^{\frac{4}{3}}\\\\y'=(x^{\frac{1}{5} })'+(x^{\frac{4}{3}})'=\frac{1}{5}x^{-\frac{4}{5}}+\frac{4}{3}x^{\frac{1}{3}}=\frac{1}{5\sqrt[5]{x^{4}}}+\frac{4\sqrt[3]{x}}{3}$

$2)y=Cos(1-x^{2} )\\\\y'=[Cos(1-x^{2})]'=-Sin(1-x^{2})*(1-x^{2})'=-Sin(1-x^{2})*(-2x)=2xSin(1-x^{2})$

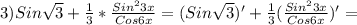
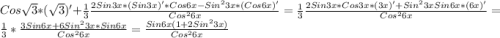
$3)Sin\sqrt{3}+\frac{1}{3}*\frac{Sin^{2}3x }{Cos6x}=(Sin\sqrt{3})'+\frac{1}{3}(\frac{Sin^{2}3x }{Cos6x})'=$$Cos\sqrt{3} *(\sqrt{3})'+\frac{1}{3}\frac{2Sin3x*(Sin3x)'*Cos6x-Sin^{2}3x*(Cos6x)' }{Cos^{2}6x}=\frac{1}{3}\frac{2Sin3x*Cos3x*(3x)'+Sin^{2}3xSin6x*(6x)' }{Cos^{2}6x }=\frac{1}{3}*\frac{3Sin6x+6Sin^{2}3x*Sin6x }{Cos^{2}6x } =\frac{Sin6x(1+2Sin^{2}3x) }{Cos^{2}6x}$