ответ:Всего
Объяснение:Обратим внимание на то, что требуется сделать букет из 7 цветов так, чтобы в нем было хотя бы три красных тюльпана, а на количество белых тюльпанов ограничений нет. Тогда, заключаем, что в букете
1) в точности 7 тюльпанов;
2) наименьшее количество красных тюльпанов 3;
3) наибольшее количество красных тюльпанов 7.
По условию количество красных тюльпанов в саду 10, то все эти 3 пункта возможны. Обозначим белые тюльпаны через 0, а красные тюльпаны через 1. Так как порядок размещения не даёт новые то получаем следующие
0000111
0001111
0011111
0111111
1111111
Всего
Объяснение:
Відповідь: правду сказали Андрій та Олеся.
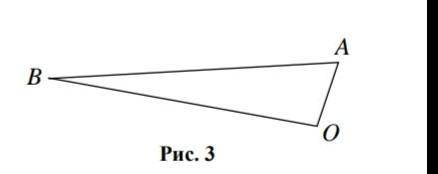
Розв’язання. Позначивши через A, B та O точки, в яких роз-
ташовуються оселі відповідно Андрія, Богдана та Олесі, за-
пишімо висловлювання друзів таким чином:
Андрій: AB AO > 2 .
Богдан: BO AB > 2 .
Олеся: BO AO > 2 .
Якщо справедливими є останні два твердження, то, додавши їх, отримаємо 2 22 BO AB AO > + , або
BO AB AO > + , що суперечить нерівності трикутника для точок A, B, O (рис. 3). А якщо справ-
джуються перше та друге твердження, то AB BO AO AB +> + 2 2 ⇒ BO AO AB AO AB > +> + 2 ,
що знову дає суперечність.
З іншого боку, перше й третє твердження справді можуть викону-
ватися водночас, якщо, наприклад, Андрій та Олеся живуть поруч,
а Богдан мешкає дуже далеко від них (як показано на рис. 3).
a_1,\ a_1+d,\ a_1+2d,\ \ldots,\ a_1+(n-1)d, \ \ldots Так что ~n-й член арифметической прогрессии равен ~{a_n}={a_1}+{ \left( n-1 \right) }d Более точно: последовательность чисел (членов прогрессии), каждое из которых, начиная со второго, получается из предыдущего добавлением к нему постоянного числа d (шага или разности прогрессии). Иначе говоря, для всех элементов прогрессии, начиная со второго, выполнено равенство: a_n=a_{n-1} + d \quad Любой член прогрессии может быть вычислен по формуле: a_n=a_1 + (n-1)d \quad \forall n \ge 1 (формула общего члена) Шаг прогрессии может быть вычислен по формуле: d=\frac{a_n-a_m}{n-m}, если n\neq m Если шаг d > 0, прогрессия является возрастающей; если d < 0, — убывающей.