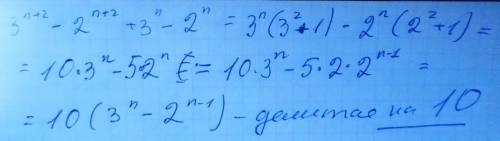
1) −0,8z5(1,2m5−2,5z) = -0.96z5m5+2z6
2) 11p3d(d3p−d3)=11p4d4−11p3d4
3) x9y2z(x2+10y2+7z2)=)x11y2z+10x9y4z+7x9y2z3
4) (4a3−3b)⋅2b−3b⋅(14a3−4b)=8a³b-6b²-42a³b+12b²= -34a³b+6b²
5) −9t2(2t5−3k)+5(4t7−2k)=-18t7+27t²k+20t7-10k=2t7+27t²k-10k
6) 13ab(14a²−b2)+14ab(b²−13a²)=182a³b-13ab³+14ab³=182a³b=ab³
10*(-2)³=10*(-8)=-80
7) 0,8(4a+3b)−6(0,3a+0,8b)=3.2a+2.4b-1.8a-4.8b=1.4а-2.4b
1.4*2-2.4*(-4)=2.8+9.6=12.4
8) 3x−ay+bz=3*(5с3+2)-3с(6с2-с+14)+15с3*(5с-1)=15с3+6-18с3+3с2-42с+75с4-15с3=75с4+(-18с3)+3с2+(-42с)+6
Объяснение:
График квадратичной функции - это парабола.
Коэффициент а отвечает за направление ветвей параболы (а>0 - ветви направлены вверх, a<0 - ветви направлены вниз).Дискриминант D отвечает за пересечение параболы с осью абсцисс (ось ОХ). D>0 - две точки пересечения, D=0 - одна точка пересечения, D<0 - точек пересечения нет.-b/2a - уравнение x₀, то есть это значение х вершины параболы.Коэффициент с отвечает за ординату (значение y) точки пересечения параболы с осью ординат (ось ОУ).Таким образом, чтобы схематично изобразить графики, нам нужно просто разобраться, как они себя ведут в конкретном случае (с сведений выше).
P.S. В четвертом случае точно имелось в виду значение с, а не D? Просто от этого меняется график.
