
![sin^4(x)+cos^4(x)=cos^2(2x)+\frac{1}{4}\\\\ sin^4(x)+2*sin^2(x)*cos^2(x)+cos^4(x)-2*sin^2(x)*cos^2(x)=\\=cos^2(2x)+\frac{1}{4}\\\\ \ \ [sin^2(x)+cos^2(x)]^2-2*sin^2(x)*cos^2(x)=cos^2(2x)+\frac{1}{4}\\\\ 1^2-\frac{1}{2}*[2*sin(x)*cos(x)]^2=cos^2(2x)+\frac{1}{4}\\\\ \frac{3}{4}-\frac{1}{2}*[sin(2x)]^2=cos^2(2x)\\\\ 3-2*sin^2(2x)=4cos^2(2x)\\\\ 3-2*[1-cos^2(2x)]=4cos^2(2x)\\\\ 3-2+2cos^2(2x)=4cos^2(2x)\\\\ 1=2cos^2(2x)\\\\ 1=2*\frac{1+cos(4x)}{2}\\\\ 1=1+cos(4x)\\\\ cos(4x)=0\\\\](/tpl/images/0910/3525/73424.png)
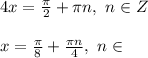
Выражение: 2*(X+Y)=5+X
ответ: X+2*Y-5=0
Решаем по действиям:
1. 2*(X+Y)=2*X+2*Y
2. 2*X-X=1*X
Решаем по шагам:
1. 2*X+2*Y-5-X=0
1.1. 2*(X+Y)=2*X+2*Y
2. X+2*Y-5=0
2.1. 2*X-X=1*X
Решаем уравнение X+2*Y-5=0:
Решаем относительно Y:
Y=(-X+5)/2=-X/2+5/2=-X/2+2.5.
Выражение: 3*(X+Y)+4*(5+Y)=-(X+Y+1)
ответ: 4*X+8*Y+21=0
Решаем по действиям:
1. 3*(X+Y)=3*X+3*Y
2. 4*(5+Y)=20+4*Y
3. 3*Y+4*Y=7*Y
4. 3*X+X=4*X
5. 7*Y+Y=8*Y
6. 20+1=21
Решаем уравнение 4*X+8*Y+21=0:
Решаем относительно Y:
Y=(-4*X-21)/8=-4*X/8-21/8=-0.5*X-21/8=-0.5*X-2.625.
( 8 * ( 12 + 18 ) ) : ( 3 - 2 )
Объяснение:
Можно увеличить значение выражения, если умножить 8 на наибольшее число. Но также благодаря делению мы можем уменьшить значение, поэтому сразу делить - плохая идея. Стоит заметить, что в конце стоит -2, и поэтому мы сможем разделить на наименьшее из возможных чисел (ну, кроме нуля, конечно), т.е на (3-2) = 1.
Итого получаем: (8*12+18):(3-2)
Выгодней будет поставить скобки так (8*(12+18)):(3-2), потому что 18 > 12, и увеличивая число, на которое мы умножаем, мы максимально увеличили произведение.
Мы максимально уменьшили делитель и максимально увеличили делимое, следовательно - (8*(12+18)):(3-2) - наибольший из возможных вариантов.