
Решаем методом замены.
Пусть x² + 4x = a, тогда получаем уравнение
a(a - 17) = -60
a² - 17a = -60
a² - 17a + 60 = 0
По теореме Виета находим корни:
a1 = 5; a2 = 12
Возвращаемся к старым переменным, учитывая, что a = x² + 4x:
x² + 4x = 5 или x² + 4x = 12
x² + 4x - 5 = 0 x1 = -6;x2 = 2
x1 = -5;x2 = 1
Таким образом, данное уравнение имеет 4 корня:
-6; -5; 1; 2
Сделаем замену сначала: 7x=t, т.е 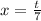
Поскольку x->0, то и 7x->0, значит и t->0.
Подставляем в наш предел то что получилось с учетом замены:
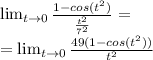
Поскольку нас неопределенность 0/0 можно использовать правило Лопиталя.
Получаем:
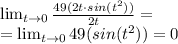
Возможно я не так понял задание и там имелось в виду:
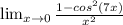
Тогда используем ту же самую замену.:
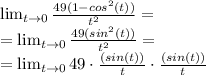
Видим что здесь произведение двух "первых замечательных пределов", а именно:
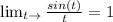
Используем этот факт и получим: 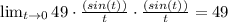
Как-то так. Но обязательно проверь.