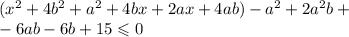
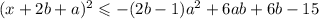
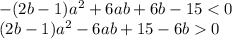
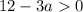
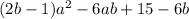должен принимать только положительные значения. Как известно, так будет, если: 1. Коэффициент при a^2 положительный и 2. Дискриминант отрицательный.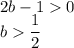
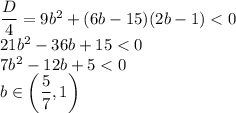
через данную точку, мы должны, взять значение икса в данной точке, и подставить данное значение в функцию:
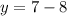
Пусть х-скорость течения реки, то
(18+х)км/ч - скорость теплохода по течению
(18-х)км/ч - скорость теплохода против течения
Составим уравнение
50 8
+ = 3 ч
18+x 18-x
50(18-х)+8(18+х) = 3(18-х)(18+х)
900-50х+144+8х-972+3x^2=0
3x^2 - 42x+72=0
D=1764-864=900>0
x1=12 км/ч
х2=2км/ч
По логике скорость течения реки не может быть 12 км/ч, зн. скорость будет 2 км/ч