y = x³ + 3x² - 45x - 2
Найдём производную :
y' = (x³)' + 3(x²)' - 45(x)' - 2' = 3x² + 6x - 45
Приравняем производную к нулю и найдём критические точки :
3x² + 6x - 45 = 0
x² + 2x - 15 = 0
По теореме Виета :
x₁ = - 5
x₂ = 3
Найдём значения функции в критических точках и на концах отрезка и сравним их .
y(- 5) = (- 5)³ + 3 * (- 5)² - 45 * (- 5) - 2 = - 125 + 75 + 225 - 2 = 173
y(3) = 3³ + 3 * 3² - 45 * 3 - 2 = 27 + 27 - 135 - 2 = - 83
y(- 8) = (- 8)³ + 3 * (- 8)² - 45 * (- 8) - 2 = - 512 + 192 + 360 - 2 = 38
y(8) = 8³ + 3 * 8² - 45 * 8 - 2 = 512 + 192 - 360 - 2 = 342
y(наим) = - 83
y(наиб) = 342
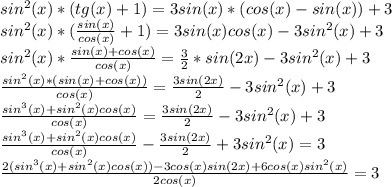
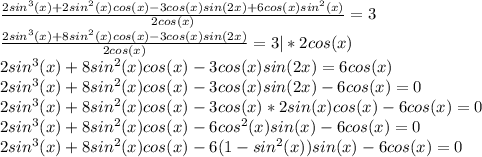
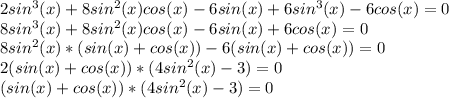
sin(x)+cos(x) = 0 или 4sin²(x)-3 = 0
sin(x) = -cos(x) |:cos(x) 4sin²(x) = 3
tg(x) = -1 sin²(x) = 3/4
x₁ = 3π/4 + πn, n∈Z sin(x) = ±√3/2
sin(x) = -√3/2 или sin(x) = √3/2
x₂ = arcsin(-√3/2) + 2πn x₄ = arcsin(√3/2) + 2πn
x₃ = π-arcsin(-√3/2) + 2πn x₅ = π-arcsin(√3/2) + 2πn
x₂ = -π/3 + 2πn x₄ = π/3 + 2πn
x₃ = π+π/3 + 2πn x₅ = π-π/3 + 2πn
x₂ = 5π/3 + 2πn, n∈Z x₄ = π/3 + 2πn, n∈Z
x₃ = 4π/3 + 2πn, n∈Z x₅ = 2π/3 + 2πn, n∈Z
Следовательно:
x₄ = π/3 + 2πn, n∈Z,
x₅ = 2π/3 + 2πn, n∈Z
ответ: x₁ = 3π/4 + πn, n∈Z;
x₄ = π/3 + 2πn, n∈Z;
x₅ = 2π/3 + 2πn, n∈Z
7-x/x-3