а) Выбрать 4 ромашки можно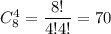 
а 3 незабудки - 
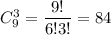По правилу произведения, составить букет из 7 цветов, в котором 4 ромашки и 3 незабудки можно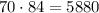 
ответ
b) Как минимум 4 незабудки это 4 незабудки или 5 незабудки или 6 незабудки или 7 незабудки.. Чувствуется что здесь правило сложения. Четыре незабудки и три ромашки можно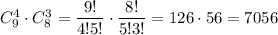 
Выбрать пять незабудки и две ромашки можно 
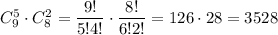Выбрать шесть цветов незабудки и одна ромашку можно 
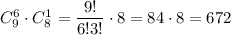И наконец выбрать семь цветов незабудки можно 
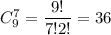По правилу сложения, составить букет из 7 цветов, в котором как минимум должны быть 4 незабудки можно 7056 + 3528+672+36=11292
ответ: 11292.
1. Сначала вычисляем общее количество возможных вариантов события. Ты можешь взять 1 из любых 41+59=100 карандашей.
А — событие, при котором ты вытягиваешь зелёный карандаш. Вариантов исходов событий — 41.
Тогда P(A)=41/100 = 0,41
2. Общее количество возможных вариантов события расстановки шаров вычисляем как 5!=1×2×3×4×5=120.
B — событие, при котором составляется верная комбинация. Вариантов исходов событий — 1.
Тогда P(B)=1/120
3. Общее число возможных вариантов события вычисляем как 5!/2! = (2!×3×4×5)/2! = 60.
С — событие, при котором число кратно 5. Число кратно 5 тогда, когда оно заканчивается единицей. Число таких событий вычисляем как 4!/2! = (2!×3×4)/2! = 12.
Тогда P(C)=12/60=1/5=0,2.
4. Вероятность того, что попадётся тетрадь в клетку в первой стопке — 2/3. Вероятность того, что попадётся тетрадь в клетку во второй стопке — 2/5.
P(F) — событие, при котором из двух пачек вытягивают тетрадь в клетку. Подсчитаем число исходов, благоприятствующих этому событию (среди 3 тетрадей 1 будет в клетку): 1 тетрадь в клетку можно взять из 4 тетрадей в клетку С при этом остальные 2 тетради должны быть в линейку; взять же 2 тетради в линейку из 6 тетрадей в линейку можно С Следовательно, число благоприятствующих исходов равно С1/4 С2/6:
Р(F)=С1/4*С2/6:С3/10= 20/72=5/18.
5. Общее число возможных вариантов событий равно 36.
D — событие, при котором сумма очков делится на 9. Таких вариантов, благоприятствующих событию, — 4 (3+6; 6+9; 5+4; 4+5).
Тогда P(D)=4/36=1/9.
Насчёт четвёртого я не уверен.
x ∈ (-∞, -3] ∪ [0,4]