Выражения 6⋅a⋅y; 0,25x3; abbc; 8,43; 16c⋅(−12)d; 38x2y тоже являются одночленами.
При записи одночленов между числами и переменными знак умножения не ставится
(6⋅a⋅y = 6ay).
Одночленом также считается:
- одна переменная, например, x, т. к. x=1⋅x;
- число, например, 3, так как 3=3⋅x0 (одно число также является одночленом).
Некоторые одночлены можно упростить.
Упростим одночлен 6xy2⋅(−2)x3y, используя свойство умножения степеней:
am⋅an=am+n —
6xy2⋅(−2)x3y = 6⋅(−2)xx3y2y=−12x4y3
(числа перемножаются, а показатели у одинаковых букв складываются)...
Объяснение:
Запишем одночлен 10⋅12abbb в стандартном виде: 10⋅12abbb=5⋅2⋅12ab3=5ab3.
 часа.
часа.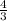 часа - 3 кг сплава
часа - 3 кг сплава кг сплава
кг сплава часа.
часа. часа - 3 кг сплава
часа - 3 кг сплава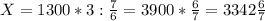 кг сплава
кг сплава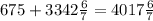 кг сплава
кг сплава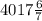 кг сплава.
кг сплава.
3х+7у=5
3*4х-3*5у=3*(-22)
4*3х+4*7у=4*5
12х-15у=-66
12х+28у=20
12х-12х+28у-(-15у)=20-(-66)
28у+15у=20+66
43у=86
у=86/43
у=2
4х-5*2=-22
4х-10=-22
4х=-22+10
4х=-12
х=-12/4
х=-3
Проверка:
4*(-3)-5*2=-12-10=-22
3*(-3)+7*2=-9+14=5
ответ: х=-3; у=2.