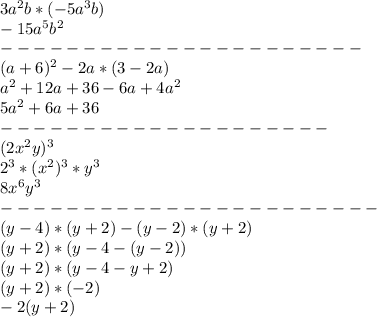
Объяснение:
Первый признак равенства треугольников:
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то треугольники равны.
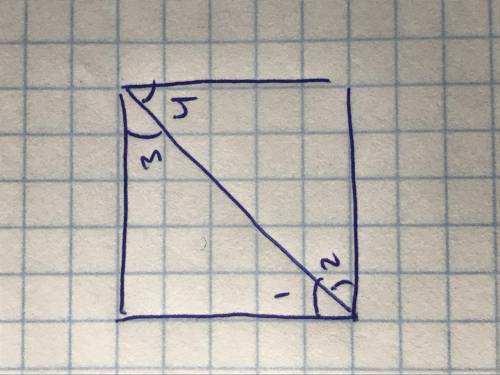
Получается, бисектриса делит квадрат на два треугольника. Треугольники, на которые бисектриса делит квадрат являются прямоугольными, так как углы у квадрата прямые. По определению у квадрата все стороны равны, то есть катеты треугольников тоже будут равны. + углы между сторонами треугольника тоже равны, они 90 градусов. Получается, по первому признаку треугольники, на которые бисектриса делит квадрат равны. А так как треугольники равны, то углы у них тоже равны. Поэтому, угол 1=2, 3=4.
Пусть A1 — центр вписанной окружности ∆ SBC, B1 — центр вписанной окружности ∆ SAC, AA1 пересекается с A, A1, B1, B лежат в одной плоскости, значит прямые AB1 и BA1 пересекаются на ребре SC. Пусть точка пересечения этих прямых — p. Так как Ap и Bp — биссектрисы углов A и B, то . Но тогда AC • BS = BC • AS, отсюда , следовательно биссектрисы углов S в ∆ ASB и C в ∆ ACB пересекаются на ребре AB, т.е. точки S, C и центры вписанных окружностей ∆ ASB и ∆ ACB лежат в одной плоскости. Отсюда следует, что отрезки, соединяющие вершины S и C с центрами вписанных окружностей противолежащих граней, пересекаются.