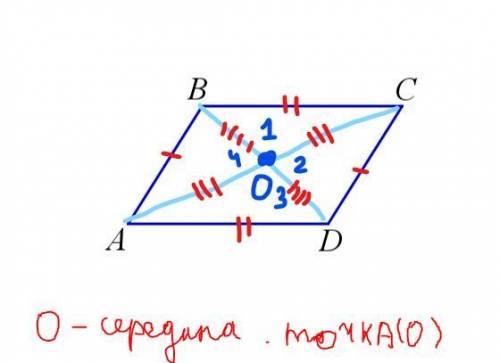
Элементы:
BC║AD
AB║CD - Стороны ABCD
∠A,∠C u ∠B,∠D - они противоположные.
Объяснение:
Свойства:
BC = AD
AD = CD ; AC∩BD в.т О.
-----------
AO = OC ; BO = OD
-----------
∠A=∠C ; ∠B=∠D - как противолежащие.
----------
∠1 u ∠4 ; ∠2 u ∠3 - как вертикальные.
--------->
P = 2*(a + b)
P = a+b+c+d
Обозначим длину прямоугольника как а, ширину прямоугольника как b, и диагональ как c.
Рассмотрим ΔABC: ∠B=90° ⇒ ΔABC - прямоугольный; a,b - катеты, c - гипотенуза
т. Пифагора гласит:
a² + b² = c²
a² + b² = 13²
a² + b² = 169
А площадь прямоугольника находится по формуле:
S = a * b
a * b = 60
Составим систему уравнений и решим методом подстановки.
Вводим новую переменную.
b² = t - новая переменная.
b² = t
b² = 25 или b² = 144
b₁ = 5; b₂=-5; b₃=12; b₄=-12
Т.к. сторона не может быть отрицательна, то -5 и -12 не подходят.
a * b = 60
a₁ * 5 = 60
a₁ = 12
a₂ * 12 = 60
a₂ = 5
⇒ Стороны прямоугольника равны 5 см и 12 см.
ответ: 5 см; 12 см
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Теоремы (свойства параллелограмма): В параллелограмме противоположные стороны равны и противоположные углы равны: , , , . ... Диагонали параллелограмма делят его на два равных треугольника.