График в файле.
Объяснение:
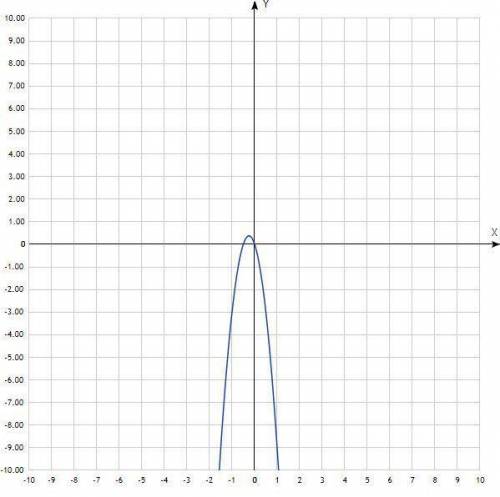
y=-6x²-3x
функция квадратичная вида ax²+bx+c - значит парабола
аргумент а - отрицательный, значит ветви параболы направлены вниз.
с=0, значит одна из ветвей пересекает ось Оу в точке с координатой у=0, если так, то и ось Ох она пересекает с координатой х=0, т.е. ветвь параболы проходит через начало координат.
находим точки пересечения с осью Ох
-6х²-3х=0
-3х(2х+1)=0
х1=0
2х+1=0
2х=-1
х2=-1/2
находим вершину параболы
х=-b/(2a)
x=3/-12=-1/4
y=-6*(-1/4)²-3*(-1/4)=3/8
(-1/4;3/8) - координаты вершины
Строим график.
Если количество элементов бесконечное, то различают разные уровни бесконечности.
На нижнем (нулевом) уровне стоят счетные множества. Математики говорят, что у них кардинальное число равно алеф-нуль.
Это, например, множества целых, натуральных или рациональных чисел.
Георг Кантор доказал, что все эти три множества - счетные, и имеют мощность алеф-нуль.
Выше, на первом уровне, стоят множества действительных чисел, комплексных чисел, а также множества точек на отрезке, на прямой, на плоскости или в пространстве.
Это Кантор тоже доказал, что каждой точке на прямой можно поставить в соответствие точку на плоскости или в пространстве.
Про эти множества говорят, что они имеют мощность алеф-один, или мощность континуума.
Так вот, мощность множества точек на отрезке любой длины, [3;8] или [0;4], или на открытом промежутке [0;4), равно мощности прямой, то есть континууму.
Обозначается английской буквой с.