Объяснение:
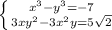
сложим эти два уравнения и преобразуем по формуле куба разности:

Для простоты вычислений введём константу С
![C=\sqrt[3]{5\sqrt{2}-7 }](/tpl/images/2018/3457/220b9.png)
C≈0,4142
Из последнего выражения имеем следующие тождества
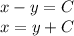
Подставляем x в первое уравнение
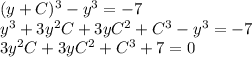
В последнее С³ подставим его значение, чтобы сократить семёрку.
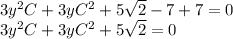
Теперь решаем обычное квадратное уравнение
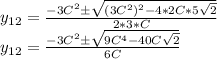
Тут получается что дискриминант отрицательный и корней нет.
Вариант второй, графический
из первого уравнения получаем график функции
![y=\sqrt[3]{x^{3} +7} \\](/tpl/images/2018/3457/4771c.png)
А из второго
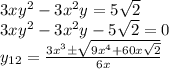
Строим графики.
Видим, что точек пересечения нет.
Графики стремятся приблизится друг к другу, но не пересекаются
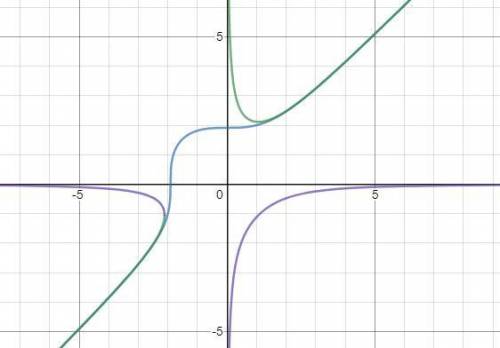
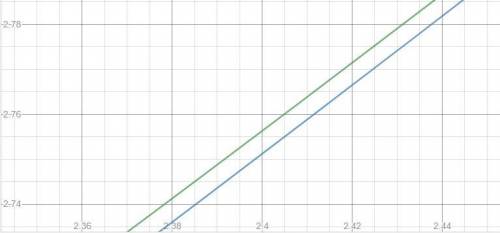
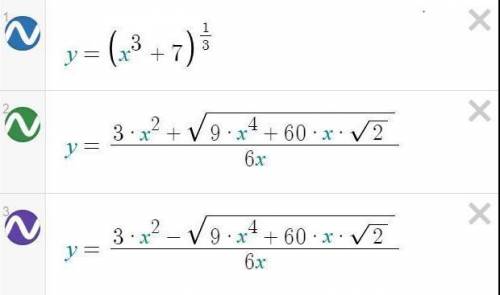
1) x² + 2x - 8 = (x - 2)(x + 4)
Для условия x² + 2 - 8:
x² + 2 - 8 = x² - 6 = (x - √6)(x + √6)
2) 3x₂ - 11x + 8 = (x - 1)(3x - 8)
Объяснение:
1) а) x² + 2x - 8
Найдем корни квадратного трехчлена по т.Виета: сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
x₁ + x₂ = -2; x₁*x₂ = -8
⇒ корни данного квадратного трехчлена x₁ = -4; x₂ = 2
Разложим выражение на множители:
x² + 2x - 8 = (x - 2)(x + 4)
б) x² + 2 - 8
Упростим выражение и найдем его корни:
x² + 2 - 8 = x² - 6
x₁ = √6; x₂ = -√6
Тогда x² + 2 - 8 = x² - 6 = (x - √6)(x + √6)
2) 3x² - 11x + 8
Найдем корни квадратного трехчлена с дискриминанта:
D = b² - 4ac = 11² - 4*3*8 = 121 - 96 = 25 = 5²
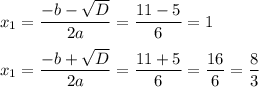
Разложим квадратный трехчлен на множители:
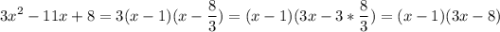
(Множитель 3 внесли во вторую скобку или вторую скобку умножили на 3).
Х=0,2 У=-2