2sin²x-7cosxsinx+5cos²x=0 [-2π;-π/2]
разделим на cos²x≠0 ⇒х≠π/2+πк, к∈Z
2tg²x-7tgx+5=0
tgx=t
2t-7t+5=0
D=49-40=9
t1=(7+3)/4=10/4=2.5
t2=(7-3)/4=4/4=1
a)tgx=1 ⇒ x=π/4+πk, k∈Z
k=0 x=π/4 - не подходит
к=-1 х=π/4-π=-3π/4 подходит
к=-2 х=π/4-2π=-7π/4 подходит
к=-3 х=π/4-3π=-11π/4 не подходит
b)tgx=2.5 ⇒ x=arctg(2.5)+πn, n∈Z
arctg2.5≈1.19
-2π≈-6.28
-π/2≈-1.57
π≈3.14
3π≈9.42
промежуток [-6.28;-1.57]
n=0 x=1.19 не подходит
n=-1 x=1.19-3.14=-1.95 подходит
n=-2 x=1.19-6.28=-5.09 подходит
n=-3 x=1.19-9.42=-8.23 не подходит
x=-1.95, x=-5.09, х=-3π/4, х=-7π/4
Пусть первоначальная скорость равна х км/ч, а после увеличения скорости - (x+12) км/ч. Время пути из пункта А в пункт В, равно 300/х ч, а из пункта В в пункт А - 300/(x+12) ч. На обратный путь автомобиль затратил на 50 мин меньше, чем на путь от А до В, значит составляем и решим уравнение
50 мин = 50/60 ч = 5/6 ч.
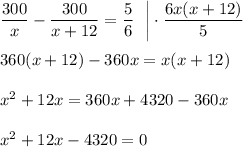
По теореме Виета
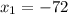— не удовлетворяет условию.
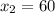км/ч - первоначальная скорость автомобиля.
ответ: 60 км/ч.
2) Найдем дискриминант квадратного уравнения
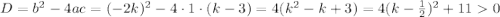
D>0 для всех действительных k имеет два действительных корня, значит нет такого значения k в котором квадратное уравнение имело бы только один корень.
3) Квадратное уравнение имеет корни(т.к.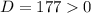 
), значит можем воспользоваться теоремой Виета.
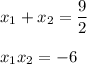
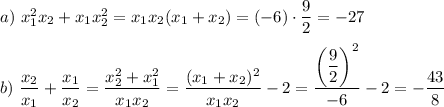
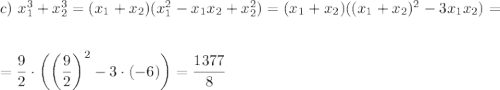
x=-5
y=-3×(-5)
y = 15