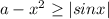
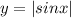расположен выше оси ОХ. 
.
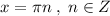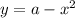- это параболы , ветви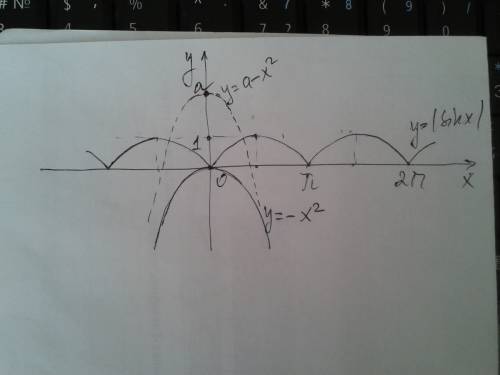
ответ:
получи подарки и
стикеры в вк
нажми, чтобы узнать больше
августа 14: 23
найти все значения а при которых сумма квадратов корней уравнения х^2+(2-а)х-а-3=0 будет наименьшей
ответ или решение1
архипова вера
рассмотрим корни уравнения: х^2 + (2 - а) * х - (а-3) = 0, и применим теорему bиета:
х1 + х2 = -(2 - а); х1 * х2 = - а - 3.(1)
найдём искомые (х1² + х2²) = (х1 + х2)² - 2 * х1 * х2.
все эти величины определены в (1). подставим значения.
х1² + х2² = [-(2 - а)]² - 2 * (- а - 3) = (2 - а)² + 2 * а + 6 = 4 - 4 * а + а² + 2 * а + 6 = а² - 2 * а + 10. (2)
в полученном выражении выделим полные квадрат.
тогда (2) примет вид: а² - 2 * а * 1 + 1² + (10 - 1) = (а - 1)² + 9. (3). проанализируем выражение (3), (а - 1)²> 0 при любых а и минимально при а = 1.
объяснение:
-π/2 <α<0 (четвертая четверть)
1) Найдем sinα
sin²α +cos²α = 1
sin²α = 1 - cos²α
sin²α = 1 - (8/17)²
sin²α = 225/289 = (15/17)²
sin α = - 15/17 (синус в четвертой четверти отрицательный)
2) ctg α = cosα/sin α
ctg α = 8/17 : (-15/17) = - 8/15
3)
ctg 2α = ((-8/15)² -1)/2·(-8/15)= (64/225-1) : (- 16/15) =
= - 161/225 * (- 15/16) = 161/240
ctg 2α = 161/240