
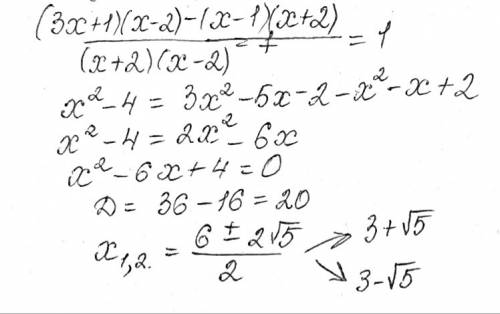
ответ:Извиняюсь что не в том порядке
Объяснение:
б) Используя cos (t)² = 1-sin (t)² запишем выражение в развёрнутом виде
1-sin (a)²/sin (a)+1
Использу а²-b²=(a-b)(a+b) разложим на множители выражение
(1-sin (a))*(1+sin(a))/sin(a)+1
Дальше мы можем сократить дробь на sin(a)+1
отсюда 1-sin(a)
a) Упростим выражение Sin^2 a/(1 + cos a).
Известно, что sin^2 a + cos^2 a = 1, тогда sin^2 a = 1 - cos^2 a. Подставим вместо sin^2 a выражение 1 - cos^2 a, тогда:
Sin^2 a/(1 + cos a) = (1 - cos^2 a)/(1 + cos a);
разложим числитель дроби на множители, используя формулу сокращенного умножения разности квадратов и получим:
(1^2 - cos^2 a)/(1 + cos a) = (1 - cos a) * (1 + cos a)/(1 + cos a);
Числитель и знаменатель дроби сокращаем на (1 + cos a) и тогда останется:
(1 - cos a) * 1/1 = 1 - cos a;
Значит, sin^2 a/(1 + cos a) = 1 - cos a.
1) (2х-у)/у 2) - 2у / (х+у) 3) 5/6с
Объяснение:
(2х/у² - 1/2х ):(1/у+1/2х)= ( приводим к общему знаменателю в каждой скобке отдельно, в первой скобке знаменатель 2ху²,во второй 2ху)
Приводим к общему знаменателю домножив первый на 2х второй член первых скобок на у², во второй скобке на 2х и второй на у.) получим
(4х² -у²)/2ху : (2х+у)/2ху =
(2х-у)(2х+у) 2ху
х = (2х-у)/у
2ху ² (2х+у)
2) сперва приведем к знаменателю а потом по формуле сокращенного умножения разложим
(х²-2ху+у²-х²+у² ) / (х-у)(х+у)= 2у(у-х) / (х-у)(х+у)= -2у(х-у) / (х-у)(х+у)
=-2у / (х+у)
(3с+2с)/6 *1/с²=5с/6с²=5/6с