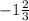В решении.
Объяснение:
Из пункта А в пункт В, расстояние между которыми 210 км, одновременно выехали два автомобиля. Так как скорость первого автомобиля на 5 км/ч больше скорости второго, то первый автомобиль в пункт назначения прибыл на 12 мин раньше, чем второй. Найдите скорость каждого из автомобилей.
Формула движения: S=v*t
S - расстояние v - скорость t – время
Таблица:
v (км/час) S (км) t (час)
1 автомобиль х 210 210/х
2 автомобиль х - 5 210 210/(х - 5)
По условию задачи разница во времени 12 минут = 0,2 часа, уравнение:
210/(х - 5) - 210/х = 0,2
Умножить все части уравнения на х(х - 5), чтобы избавиться от дробного выражения:
210х - 210х + 1050 = 0,2х² - х
-0,2х² + х + 1050 = 0
Разделить все части уравнения на -0,2 для упрощения:
х² - 5х - 5250 = 0, квадратное уравнение, ищем корни:
D=b²-4ac = 25 + 21000 = 21025 √D=145
х₁=(-b-√D)/2a
х₁=(5-145)/2 = -140/2 = -70, отбросить, как отрицательный;
х₂=(-b+√D)/2a
х₂=(5+145)/2
х₂=150/2
х₂=75 (км/час) - скорость первого автомобиля;
75 - 5 = 70 (км/час) - скорость второго автомобиля;
Проверка:
210 : 75 = 2,8 (часа);
210 : 70 = 3 (часа);
3 - 2,8 = 0,2 (часа) - верно.
Объяснение:
№1
А) (2х+1)²= 4х²+4х+1
Б) (3а-с)²= 9а²–6ас+с²
В) (а+6)(а-6)= а²–36
Г) (3х-4у) (3х+4у)= 9х²–16у²
№2
А) у²-¼= (у–½)(у+½)
Б) х²+10х+25= (х+5)²
№3
(2х-у)²-4х(х-у)= 4х²–4ху+у²–4х²+4ху= у²
при у= -⅔
(–⅔)²=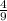
ответ: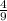
№4
А) 3(2а-b) (2a+b)= 3(4a²–b²)= 12a²–3b²
Б (х⁴+у³)² = (x^8)+2x⁴y³+(y^6)
В) (а+3b)²-(a-3b)²=(a+3b+a–3b)(a+3b–(a–3b))= a²(a+3b–a+3b)= a²*6b= 6a²b
№5
А) (2а-5)²-(2а-3) (2а+3)=0
(4a²–20a+25)–(4a²–9)=0
4a²–20a+25–4a²+9=0
–20a+34=0
20a=34
a=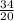
a= 1,7
Б) 9с²-25=0
(3c–5)(3c+5)=0
совокупность:
3с–5=0
3с+5=0
совокупность:
3с=5
3с=–5
совокупность:
с=
с=
совокупность:
с=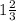
с=