Экстремумы на отрезке находятся либо в стационарных точках (точках, где производная функции обращается в ноль), либо на концах отрезка.
Для этого сначала нужно найти производную функции. Если я правильно поняла запись Вашей функции и она такая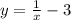
То ее производная равна -1/х^2
Критической точкой здесь будет х=0. Но наша функция в этой точке не существует. Значит экстремумы находятся на концах отрезка:
у(-1)=-4
у(1)=-2
Значит минимальное значение функция достигает в точке х=-1 и равна -4.
Максимальное значение функции на отрезке равно -2 и находится в точке х=1.
8sinx*cosx-3cosx^2+3sinx^2=3
8sinx*cosx-3cosx^2+3(1-cosx^2)=3
8sinx*cosx-6cosx^2+3=3
8sinx*cosx-6cosx^2=0
2cosx*(4sinx-3cosx)=0
Cosx=0 x=pi/2 +pin
Или 4sinx-3cosx=0 x=arctg 3/4 +pin