Найти стороны прямоугольника.
Стороны прямоугольника обозначим через "х" и "у" .
Периметр прямоугольника равен Р=2(х+у)=160 ⇒ х+у=80 .
Когда увеличили одну сторону (пусть это будет сторона "х") на 40%, то есть на 0,4 части, то она стала равна (1+0,4)*х=1,4х .
Когда уменьшили вторую сторону на 40%, то есть на 0,4 части, то сторона стала равной (1-0,4)*у=0,6у .
Периметр такого прямоугольника уменьшился на 10%, то есть на 0,1 части, и стал равным (1-0,1)*Р=0,9*160=144 .
Теперь периметр прямоугольника равен 2(1,4х+0,6у)=144 ⇒
1,4х+0,6у=72 .
Решаем систему:
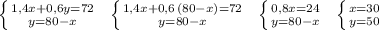
Стороны первого прямоугольника равны 30 см и 50 см, а стороны изменённого прямоугольника равны 1,4*30=42 см и 0,6*50=30 см .
Угол B:
Угол C:
Теперь найдем по порядку площади трех треугольников KBM, MLC, AKL:
Но прежде, по свойству биссектрис определим, что AK=8/9, BK = 10/9, BM = 5/3, MC = 10/3, LC = 20/7, AL = 8/7;
Треугольник AKL:
Треугольник MLC:
Треугольник MBK:
Если из площади треугольника ABC вычесть сумму трех найденных площадей, то мы найдем площадь треугольника MKL; Пусть сумма трех площадей равна N; Тогда: