Дано уравнение: , где и - корни уравнения. найти p если -=, а корни положительны.

👇

Увидеть ответ

Ответ:

culi42

30.09.2020

по теореме кого-то там (из головы вылетело)

p=-(x1+x2)

по условию

х1-х2=2*root(2)

D=p^2-28

x1=1/2*(-p+root(p^2-28))

x2=1/2*(-p-root(p^2-28))

x1-x2 = root(p^2-28) = 2*root(2)

p^2-28 = 8

P^2 = 36

p=+-6

корни положительны, берем меньший

x2=1/2*(-p-root(p^2-28)) = 1/2*(-+6-2*root(2)) = -+3-root(2)

если будет -3 то корень меньше нуля, значит убираем этот вариант

p=-6

4,8(24 оценок)

Открыть все ответы

Ответ:

Mallony

30.09.2020

Коэффициент подобия по определению считается по линейным размерам .

Для периметра (сумме линейных размеров) он равен k, для площадей k^2,

для объемов k^3.Тогда периметр равен 12*4=48 см, площадь равна 9*4^2=144 кв. см

Как-то так

Объяснение:

Отношение периметров двух подобных треугольников равно коэффициенту подобия.

P(ABC)P(RTG)=k20P(RTG)=19P(RTG)=9⋅20=180(см)

Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

S(ABC)S(RTG)=k26S(RTG)=(19)26S(RTG)=181S(RTG)=6⋅81=486(см2)

4,8(29 оценок)

Ответ:

pudova20001katya

30.09.2020

Так как EC - биссектриса, то:
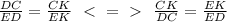
$\frac{DC}{ED} = \frac{CK}{EK} \ \ \textless \ =\ \textgreater \ \ \frac{CK}{DC}= \frac{EK}{ED}$
при делении точкой отрезка на 2 части, относящиеся как m к n, есть формула для вычисления координат этой точки:
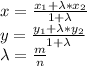
$x= \frac{x_1+\lambda *x_2}{1+\lambda} 
\\y= \frac{y_1+\lambda *y_2}{1+\lambda} 
\\\lambda= \frac{m}{n}$
ищем длины сторон:
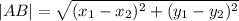
для этого используем формулу $|AB|=\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
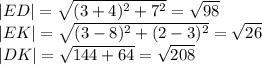
$|ED|=\sqrt{(3+4)^2+7^2}=\sqrt{98}
\\|EK|=\sqrt{(3-8)^2+(2-3)^2}=\sqrt{26}
\\|DK|=\sqrt{144+64}=\sqrt{208}$
находим координаты точки C:
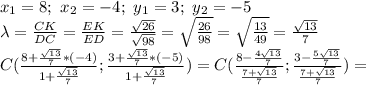
$x_1=8;\ x_2=-4;\ y_1=3;\ y_2=-5
\\\lambda= \frac{CK}{DC} = \frac{EK}{ED} = \frac{\sqrt{26}}{\sqrt{98}}=\sqrt{ \frac{26}{98} }=\sqrt{ \frac{13}{49} } = \frac{\sqrt{13}}{7} 
\\C( \frac{8+ \frac{\sqrt{13}}{7} *(-4)}{1+ \frac{\sqrt{13}}{7}} ; \frac{3+ \frac{\sqrt{13}}{7}*(-5)}{1+ \frac{\sqrt{13}}{7}} )=C( \frac{8- \frac{4\sqrt{13}}{7} }{ \frac{7+\sqrt{13}}{7} } ; \frac{3- \frac{5\sqrt{13}}{7} }{\frac{7+\sqrt{13}}{7}} )=$
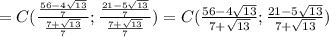
$=C( \frac{ \frac{56-4\sqrt{13}}{7} }{\frac{7+\sqrt{13}}{7}}; \frac{ \frac{21-5\sqrt{13}}{7} }{\frac{7+\sqrt{13}}{7}})=C( \frac{56-4\sqrt{13}}{7+\sqrt{13}} ; \frac{21-5\sqrt{13}}{7+\sqrt{13}} )$
теперь определим вид треугольника для этого используем теорему косинусов:
вид треугольника будем определять по косинусу самого большого угла; если cos<0, то угол тупой; если cos=0, то угол прямой; если cos>0, то угол острый.
Против большей стороны лежит больший угол, поэтому запишем теорему косинусов для DK и косинуса угла E:
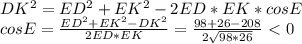
$DK^2=ED^2+EK^2-2ED*EK*cosE
\\cosE= \frac{ED^2+EK^2-DK^2}{2ED*EK} = \frac{98+26-208}{2\sqrt{98*26}}\ \textless \ 0$
cosE<0 поэтому угол тупой и треугольник тупоугольный
ответ:
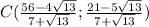
1) $C( \frac{56-4\sqrt{13}}{7+\sqrt{13}} ; \frac{21-5\sqrt{13}}{7+\sqrt{13}} )$
2) треугольник тупоугольный

4,6(72 оценок)

Это интересно:

Стиль-и-уход-за-собой

04.06.2022

5 главных секретов ухода за недавно сделанным пирсингом ушей...

Компьютеры-и-электроника

12.02.2023

Как удалить временные файлы в Windows 7: Простые способы и полезные советы...

Дом-и-сад

16.05.2021

Как заменить шнурки в жалюзи - простой и быстрый способ...

19.08.2022