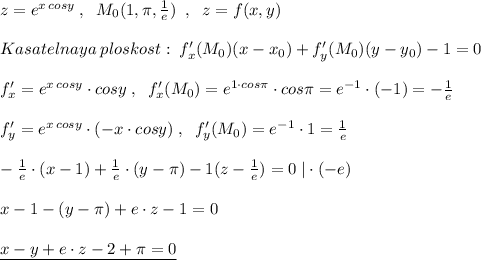
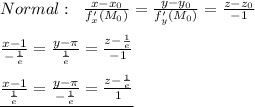
на 2) Разлагаем на множители левую часть уравнения.
Пусть u=sin(x)
. Подставим u везде вместо sin(x)
u2+5u+4
Разложим u2+5u+4на множители с группировки.
Рассмотрим x2+bx+c
. Найдем пару целых чисел, произведение которых равно c, а сумма равна b. В данном случае произведение равно 4, а сумма равна 5.
1;4
Запишем разложение на множители, используя эти целые числа.
(u+1)(u+4)
Заменим все uна sin(x)
(sin(x)+1)(sin(x)+4)
Заменим левую часть на выражение, разложенное на множители.
(sin(x)+1)(sin(x)+4)=0
Если любой отдельный множитель в левой части уравнения равен 0, то и все выражение будет равняться 0
sin(x)+1=0
sin(x)+4=0
Приравняем первый множитель к 0и решим.
Приравняем первый множитель к 0
sin(x)+1=0
Вычтем 1из обеих частей уравнения.
sin(x)=−1
Упростим выражение, чтобы найти первое решение.
Найдем обратный синус от обеих частей уравнения, чтобы извлечь x
из-под синуса.
x=arcsin(−1)
Точное значение arcsin(−1)равно −π2.
x=−π2
Функция синуса принимает отрицательные значения в третьем и четвертом квадрантах. Для определения второго решения вычитаем решение из 2π, чтобы найти угол приведения. Затем прибавляем данный угол приведения к π, чтобы найти решение в третьем квадранте.
x=2π+π2+π
Упростим выражение, чтобы найти второе решение.
Упростим правую часть.
Для записи 2π1в виде дроби с общим знаменателем, умножим ее на 22.
x=2π1⋅22+π2+π
Запишем каждое выражение с общим знаменателем , умножив на подходящий множитель 1
Скомбинируем.
x=2π⋅21⋅2+π2+π
Умножим 2на 1.
x=2π⋅22+π2+π
Скомбинируем числители с общим знаменателем.
x=2π⋅2+π2+π
Упростим числитель.
Умножим 2на 2
.
x=4π+π2+π
Складываем 4πи π.
x=5π2+π
Для записи π1в виде дроби с общим знаменателем, умножим ее на 22.
x=5π2+π1⋅22
Запишем каждое выражение с общим знаменателем 2, умножив на подходящий множитель 1
Скомбинируем. x=5π2+π⋅21⋅2
Умножим 2на 1.
x=5π2+π⋅22
Скомбинируем числители с общим знаменателем.
x=5π+π⋅22
Упростим числитель.
Перенесем 2в левую часть выражения π⋅2.
x=5π+2⋅π2
Умножим 2на π.
x=5π+2π2
Складываем 5π и 2π.
x=7π2
Вычтем 2πиз 7π2.
x=7π2−2π
Результирующий угол 3π2
котерминален углу 7π2, положителен, и его величина менее 2π.
x=3π2
Найдем период.
Период функции можно вычислить с
2π|b|
Подставим 1 вместо b в формуле для периода.
2π|1|
Решим уравнение.
Модуль - это расстояние между числом и нулем. Расстояние между 0
и 1 равно 1.
2π1
Делим 2π на 1.
2π
Прибавим 2π к каждому отрицательному углу, чтобы получить положительные углы.
Нажмите, чтобы отобразить меньше шагов...
Прибавим 2π к −π2, чтобы найти положительный угол.
−π2+2π
Для записи 2π 1 в виде дроби с общим знаменателем, умножим ее на 22.
2π122−π2
Запишем каждое выражение с общим знаменателем 2, умножив на подходящий множитель 1
Скомбинируем.
2π⋅21⋅2−π2
Умножим 2на 1.
2π⋅22−π2
Скомбинируем числители с общим знаменателем.
2π⋅2−π2
Упростим числитель.
Умножим 2на 2.
4π−π2
Вычтем π из 4π.
3π2
Запишем новые углы.
x=3π2
Период функции sin(x)равен 2π, то есть значения будут повторяться через каждые 2π радиан в обоих направлениях.x=3π2±2πn;3π2±2πn
Объединяем ответы.
x=3π2±2πn
Приравняем следующий множитель к 0и решим.
Приравняем следующий коэффициент к 0.sin(x)+4=0
Вычтем 4из обеих частей уравнения.
sin(x)=−4
Область значений синуса: −1≤y≤1
. Поскольку −4не попадает в этот интервал, решений нет.
Нет решения
Итоговым решением являются все значения, обращающие (sin(x)+1)(sin(x)+4)=0в верное тождество.
x=3π2±2πn
на
Признак делимости на 11:
Заметим, что 10...0 (в числе четное число нулей) дает остаток 1 при делении на 11: например, 1000000 = 1 + 99 99 99, разность между такой степенью десятки и 1 разбивается на группы 99-ок и поэтому делится на 99 (и, соответственно, на 11).
Если в числе 10...0 нечетное число нулей, то оно будет давать остаток 10 при делении на 11: например, 10000000 = 10 + 99 99 99 0, так же и в любой другой степени, разность между числом и 10 будет содержать какое-то количество групп 99-ок и 0, разность делится на 11.
Осталось расписать число в виде суммы разрядных слагаемых:
и заметить, что эта сумма даёт такой же остаток при делении на 11, что и
В первой скобке стоит разность сумм цифр, стоящих на четных и на нечетных местах, второе слагаемое - делится на 11. Чтобы вся сумма делилась на 11, необходимо и достаточно, чтобы разность сумм цифр, стоящих на четных и на нечетных местах, делилась на 11.
Признак делимости на 13:
Число равно 10A + b, A - число, образованное всеми цифрами кроме последней, b - последняя цифра. Утверждается, что если сложить число десятков A с учетверенным числом единиц 4b, то полученная сумма A + 4b делится на 13 тогда же, когда и исходное число. Это следует из того, что (10A + b) + 3(A + 4b) = 13(A + b); если одно слагаемое делится на 13, то и второе обязано делиться на 13, так как вся сумма делится на 13.